2. 山东科汇电力自动化股份有限公司, 山东 淄博 255087
2. Shandong Kehui Power Automation Co.Ltd., Zibo, Shandong 255087, P. R. China
安全可靠的输电线路直接影响人们的生产生活[1-2]。绝缘子作为架空线路中固定导线的重要部件, 承受极高的电压, 时常发生自爆事故, 严重威胁输电线路的安全运行[3-4]。利用无人机或直升机拍摄输电线路视频, 人工标注自爆绝缘子位置的模式, 已成为现代输电线路人工巡检技术发展的方向。然而, 人工标注过程中不同人员的主观因素, 加之巡检过程成本的客观因素, 使得巡检效果不佳。因此, 研究绝缘子状态的自动识别方法具有重要的实践意义。
国内外学者针对绝缘子状态检测展开了大量研究。文献[5]针对航拍巡检图像, 提出了一种基于SURF关键点和关联矩阵聚类的绝缘子定位识别算法。文献[6]针对高速铁路沿线悬链绝缘子, 提出了一种基于轮廓变换和Chan-Vese模型的定位与识别算法。然而, 受制于环境和识别算法等客观因素, 难以从复杂野外图像中提取有明确映射关系的状态特征, 识别模型的泛化性不强[7-9]。
从人工智能[10-11]的角度来看, 人工巡检模式是具有丰富经验的巡检员、面对未知待绝缘子图像、不断推敲比对多尺度图像全局和局部知识空间, 评判绝缘子状态。然而, 这种从全局到局部主观模式很难保证状态估量的一致性。不同样本具有不同尺度的特征需求, 传统开环决策模式识别系统具有不确定输入和不确定输出, 特征空间尺度和认知准则一旦训练完毕不再更新, 以及不确定认知结果通过后验评测其可信度, 使得其无法模仿人类思维模式, 即实时评估认知结果的可信度, 对多尺度特征空间进行自寻优调节。
随着神经网络算法的本质改进, 识别目标细节的深度学习技术受到了广泛关注[12-15]。不同于一般的识别, 图像细节识别应该能够定位和表征目标之间的细微差异。已有细节识别通常包括两个步骤:1)通过分析卷积响应确定可能的目标区域, 2)提取每个区域可区分特征并将其编码以识别。然而, 所学习的区域可能不是机器分类的最佳选择[16], 局部区域的细微视觉差异依然难以学习, 加之同属开环认知模式的固定尺度特征空间, 以及交叉熵损失函数泛化能力的不足, 机器学习的可达性和可靠性难以令人满意。
为了应对上述挑战, 模仿人工巡检模式, 即实时评估认知结果可信度自寻优调节多尺度图像知识空间决策, 笔者给出了一种基于注意力机制的绝缘子状态反馈认知方法。首先, 设计了自适应尺度堆叠的卷积神经网络架构, 使得网络输入由整体绝缘子图像缩放至细节局部区域, 确保不同分辨率输入的可区分能力并为下一尺度生成一个细节注意区域。其次, 面向多个尺度特征, 采用随机配置网络(stochastic configuration networks, SCN) [17]建立具有万局逼近能力的绝缘子状态分类准则。最后, 构建类间分类和类内尺度间排序损失函数优化注意力网络, 并借鉴闭环控制思想定义广义误差熵性能指标, 实时评测绝缘子不确定状态认知结果可信度以动态调节网络尺度等级, 实现特征空间自优化调节和分类准则重构, 反馈再认知绝缘子状态。实验结果表明了本文方法的可行性和有效性。
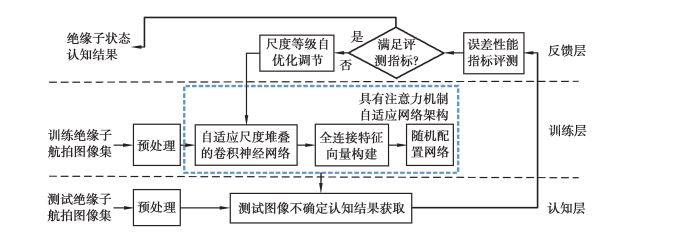
1 基于注意力机制的绝缘子状态反馈认知模型如图 1所示, 提出一种基于注意力机制的绝缘子状态反馈认知模型, 采用耦合的机制实现训练层、认知层和反馈层信息实时交互。
|
图 1 基于注意力机制的绝缘子状态反馈认知模型构建 Fig. 1 Construction o ffeedback cognition model of insulator state based on attention mechanism |
训练层包括预处理、自适应尺度堆叠的卷积神经网络、全连接特征向量构建和随机配置网络等模块。对训练航拍图像进行绝缘子串定位和分割, 获取299 ×299的绝缘子训练集。基于堆叠的卷积神经网络结构, 由反馈层误差性能评测指标下达的自适应尺度, 动态增加堆叠的多尺度卷积层获取更细节的特征空间, 随机配置网络面向全连接特征认知训练绝缘子图像的状态。
1.2 认知层面向训练层提供的自适应尺度特征空间和分类准则构建原则, 认知层针对测试绝缘子图像, 可以获取特定尺度下的不确定状态认知结果。
1.3 反馈层反馈层包括误差性能指标评测建立和尺度等级自优化调节等模块。面向认知层提供的反馈决策信息, 反馈层定义误差性能评测指标, 实时评测测试绝缘子图像状态的不确定认知结果是否满足可信度指标, 自优化调节尺度等级, 重构不满足性能指标的测试样本更深细节特征空间及其分类准则, 以再认知状态。
2 图像预处理 2.1 图像旋转在巡检过程中, 无人机或直升机时常会遭遇气流或处于不同航拍角度, 为增强学习模型面对上述情形的鲁棒性, 如图 2所示对训练集的每幅航拍图像分别进行±5°、±10°和镜像旋转。

|
图 2 航拍绝缘子图像方位旋转 Fig. 2 Rotation of aerial insulator image direction |
绝缘子航拍图像会处于不同航拍距离和角度, 首先需要在航拍图像中确定绝缘子串位置。YOLO作为一种性能优异的目标检测算法, 如图 3所示, 采用9种尺度的先验框可快速预测输入图像的目标。

|
图 3 基于YOLO的绝缘子串定位 Fig. 3 Location ofinsulator based on YOLO |
由于距离和角度的因素, 绝缘子串定位分割后具有不同的方向和大小, 需要进行归一化处理。选取定位分割后的绝缘子串图像的较短边, 将其定为299, 较长边随较短边等比例缩放。深层网络通常需要输入正方形, 设归一化后的较长边和较短边分别为A和B, 将绝缘子串图像分割为C(C=A/B)个正方形, 其中.为取整操作。若分割至最后一步时步长小于B, 则从末端向回平移B。最终, 归一化的绝缘子图像大小为299×299。
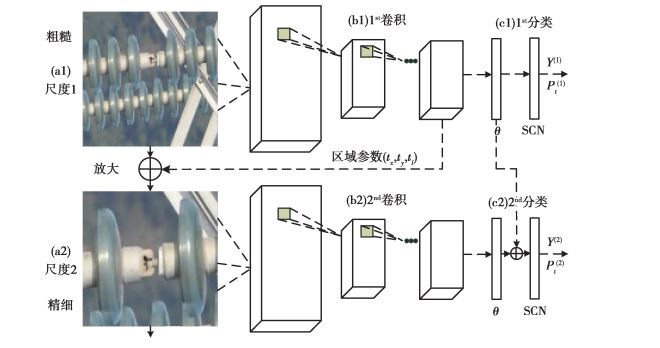
3 自适应尺度堆叠卷积神经网络本节将介绍自适应尺度堆叠卷积神经网络用于细节图像识别。以图 4包含2个尺度网络为例, 更细尺度以类似方式堆叠。输入采用递归模式, 由a1的全尺寸图像到a1中细节可区分的a2区域。首先。不同尺度的图像被送入卷积层(b1至b2)提取基于区域的特征表示。其次, 网络通过全连接层和SCN层(c1至c2)预测概率得分, 以及获取关注区域。自适应尺度堆叠卷积神经网络基于交替学习每个尺度的分类损失和相邻尺度排名损失进行优化收敛。
|
图 4 自适应尺度堆叠神经网络流程图 Fig. 4 The framework of stacked neural network with adaptive scale |
面对细节识别任务, 传统基于局部区域的框架无法有效的进行定位和识别。借鉴启发区域网络(RPN) [18], 给出了一种多尺度堆叠卷积神经网络, 其中区域的关注度几乎不占用计算资源, 并且可以端到端训练。
给定一幅输入图像X, 首先通过将X输入预训练的卷积层提取区域的深层特征Wc * X, 其中*表示卷积、池化和激活操作集, Wc表示全体参数。进一步地, 在每个尺度对具有2个输出的网络进行建模。第一个任务是生成细节类别的概率分布
| $ p(\mathit{\pmb{X}}) = g({W_{\rm{c}}}*\mathit{\pmb{X}}), $ | (1) |
式中:g (·)表示全连接层映射卷积特征至一个可匹配输出类别的特征向量, 并包括一个SCN层将特征向量转换为概率。第二个任务则是预测更细尺度关注区域的坐标。通过搜索原始图像中在最后一个卷积层具有最高响应值的区域(即VGG-19的conv5_4)来选取正方形关注区域{tx, ty, tl }, tx和ty分别表示区域的中心坐标, tl表示边长的一半。类似的方式可以分析第二个尺度的卷积响应获取更小的关注区域。一旦获取关注区域, 将其放大至299×299。
3.2 随机配置网络算法机器学习模型的基本需求是其学习表征能力。CNN中softmax损失函数逼近能力不足, 将随机权网络结合深度学习框架的工作日益受到人们的关注。面向多层感知机模型, 采用随机算法对其训练的步骤通常是在预定的区间内随机设置参数, 以等概率构建输入层与隐含层之间的权值矩阵, 最后采用最小二乘法计算隐含层与输出层之间的权值向量。然而, 随机权向量函数连接网络(random vector functional-link net, RVFL)模型的逼近能力不确定, 根本原因是其随机参数设置与建模数据无关。SCN则通过在自适应区间内, 根据输出误差约束条件设置输入层与隐含层之间的参数, 以生成新隐含层节点的随机基函数, 使得学习模型具有非线性映射关系的万局逼近能力。设θ = {θ1, θ2, …, θz }为全连接特征, Y' = [y'1, …, y'z]为真实类别, y'i = [y'i, 1, …, y'i, v], Z是样本个数, ν是样本类别个数, 则
| $ {f_L}(\mathit{\pmb{\theta}} ) = \sum\limits_{j = 1}^L {} {\rm{ }}{\beta _j}{k_j}({\varphi _j}^T\mathit{\pmb{\theta}} + {b_j}), $ | (2) |
式中:β = [β1, β2, …, βL]是输出层权值, φj和bj是随机的输入层权值和隐含层偏移, φj, bj ∈ [-λ, λ], 基函数k (·)选择sigmoid; L是隐含层节点个数。
当递增至第L个隐含层节点时, 采用如下约束条件对φL和LbL进行取值,
| $ \varepsilon L, q = \frac{{e_{L - 1, q}^T(\mathit{\pmb{\theta}} ) \bullet {a_L}{{(\mathit{\pmb{\theta}} )}^2}}}{{a_L^T(\theta ) \bullet {a_L}(\mathit{\pmb{\theta}} )}} - (1 - r - {u_L})e_{L - 1, q}^T(\mathit{\pmb{\theta}} ){e_{L - 1, q}}(\mathit{\pmb{\theta}} ), $ | (3) |
式中:q =1, 2, …, ν, 0<r<1, uL = (1-r)/ (L +1), aL (θ) = [kL (φLTθ1 +bL), …, kL (φLTθN +bL)]T表示输入数据第L个隐含层节点的激活, 则隐含层输出矩阵表示为GL = [a1, …, aL], eL-1, q (θ)为在增加第L个隐含层节点前, 输出数据关于输出层第q个节点的残差。β* = [β1*, β2*, …, βL*]T计算如下:
| $ \mathit{\pmb{\beta}} {\rm{* = }}\arg \;\mathop {{\rm{min}}}\limits_\mathit{\pmb{\beta}} \;{\rm{||}}\;{\mathit{\pmb{G}}_L}\beta - \mathit{\pmb{Y}}{\rm{'}}||_{\rm{F}}^2 = G_L, $ | (4) |
式中:GL†表示GL的广义逆, ||F表示Frobenius范数, Y = [y1, …, yz], yi = [yi, 1, …, yi, v]表示SCN的输出矩阵[17]。
3.3 分类和排序这里通过两种类型损失函数, 即尺度内分类损失和尺度间排序损失, 对多尺度堆叠卷积神经网络进行优化, 以生成注意区域和学习更细节特征。具体来说, 最小化如下目标函数,
| $ e(\mathit{\pmb{X}}) = {e_{{\rm{cls}}}}(\mathit{\pmb{Y}}',{\mathit{\pmb{Y}}^{(s + 1)}}) + {e_{{\rm{rank}}}}({p_t}^{(s)},{p_t}^{(s + 1)}), $ | (5) |
式中:s表示尺度; Y (s+1)表示特定尺度的预测向量; ecls表示分类损失, 主要用于优化图 4中的卷积层和SCN分类层参数, 以确保当前尺度具有充分的区分能力。此外, 排序损失erank中的pt(s)表示正确类别t的预测概率。erank的定义如式(6)所示。
| $ {e_{{\rm{rank}}}}({p_t}^{(s)},{p_t}^{(s + 1)}) = {\rm{max}}\{ 0,{p_t}^{(s)} - {p_t}^{(s + 1)} + \eta \} $ | (6) |
式中, 在训练中强制pt(s+1) >pt(s)) +η。这样的设计可以使网络以粗略尺度的预测为参考, 通过更细节的网络生成更可信的预测, 逐渐逼近最具可区分性的关注区域。
一旦每个尺度的堆叠卷积神经网络训练后, 可以获取从全尺寸图像X到多个由粗到细关注区域的多尺度表征,
| $ \{ {\mathit{\pmb{\theta}} _1}, {\mathit{\pmb{\theta}} _2}, {\rm{ }} \ldots {\rm{ }}, {\mathit{\pmb{\theta}} _R}\} {\rm{ }}, $ | (7) |
式中:θi表示特定尺度的全连接特征向量, R是尺度总数。为了利用集成特征的优势, 将每个尺度归一化的全连接特征向量首尾连接后, 送入最细尺度网络的SCN获取最终分类认知结果。
3.4 网络参数调节多尺度堆叠卷积神经网络需要迭代参数以更好的定位关注区域和生成泛化的特征空间及其分类准则。采用如下优化策略:
步骤1:前向传播过程中, 在反馈层误差性能指标下达的尺度等级条件下, 首先使用相同的预训练VGG网络初始化图 4中的卷积层(b1至b2和c1至c2), 获取输入绝缘子图像特定尺度的特征空间。然后, 根据公式(2) ~(4), SCN中隐含层节点个数逐渐增加, 直至达到最大个数或ecls的误差域值, 生成绝缘子状态认知结果。此外, 通过搜索原始图像中最后一个卷积层具有最高响应值的区域来选取正方形关注区域{tx, ty, tl }, 将其放大至299×299, 并计算erank, pt(0) =0。
步骤2:若目标函数e尚未达到最小, 同时隐含层节点个数已经增至最大, 启动反向更新过程, 反向传播SCN的输出误差, 以更新多尺度堆叠卷积神经网络的参数。
步骤3:交替重复上述过程, 更新特征空间并重新训练SCN, 直至目标函数e不再改变为止, 输出最终状态认知结果。
特别地, 对于SCN的反向更新, 需要分别对输出层权值、隐含层权值、隐含层偏移求导, 实现输出误差从SCN的输出端至输入端的传播:
| $ {e_{{\rm{cls}}}} = \sqrt {\frac{1}{L}\sum\limits_{j = 1}^L {{{({y_j} - y{'_j})}^2}} } , $ | (8) |
| $ k(x) = \frac{1}{{1 + {\rm{exp}}( - x)}}, $ | (9) |
| $ \frac{{\partial {e_{cls}}}}{{{\partial _{\beta j}}}} = \frac{{\partial {e_{cls}}}}{{\partial {y_j}}}*\frac{{\partial {y_j}}}{{\partial {\beta _j}}} = \frac{{{y_j} - y{'_j}}}{{\sqrt {{{({y_j} - y{'_j})}^2}} }} \bullet {a_j}, $ | (10) |
| $ \frac{{\partial {e_{cls}}}}{{\partial {\varphi _j}}} = \frac{{{y_j} - y{'_j}}}{{\sqrt {{{({y_j} - y{'_j})}^2}} }} \bullet {\beta _j} \bullet {x_j}(1 - {x_j}) \bullet \theta , $ | (11) |
| $ \frac{{\partial {e_{{\rm{cls}}}}}}{{\partial {b_j}}} = \frac{{{y_j}{\rm{ - }}{y_j}'}}{{\sqrt {{{({y_{j{\rm{ - }}}}{y_j}')}^2}} }}{\rm{\cdot}}{\beta _j}{\rm{\cdot}}{x_j}(1 - {x_j}){\rm{\cdot}}\mathit{\pmb{\theta}} , $ | (12) |
对于多尺度堆叠卷积神经网络的反向更新, 采用与VGG一致的策略, 逐层计算SCN输入端反向传播过来的误差对权值的偏导数。
4 绝缘子状态反馈认知机制面向未知绝缘子图像, 基于多尺度堆叠卷积神经网络可以获取其状态的不确定认知结果。为了模仿人工巡检模式, 在自优化调节自适应尺度特征空间以及重构分类准则之前, 需要定义误差指标实时评估不确定认知结果的可信度, 以提供量化依据再认知不确定状态。
4.1 不确定认知结果的语义误差熵评测指标设测试绝缘子图像集U, Ui ∈U, i ∈ [1, Z], 在第ω次反馈认知中, 面向尺度为s的全连接特征向量θi, sω, 其不确定状态认知结果为yi, sω ∈ [1, ν]。基于潜在语义分析可将θi, sω映射为潜在语义向量ρiw, s =[ρiw, 1, s, …, ρiw, μ s]。将ρiw, s与训练集中具有相同类别样本的潜在语义向量矩阵dyi, sω相减, 构建类内不确定认知结果误差矩阵Di, sω,
| $ \mathit{\pmb{D}}_i^\omega {, _s} = {1_{\mu \times 1}} \times \mathit{\pmb{\rho}} _i^\omega {, _s} - {\mathit{\pmb{d}}_y}_i^\omega {, _s} $ | (13) |
同理可获取ρi, sω, 与其他类别训练样本集的潜在语义误差矩阵Di, sw, *, 则Ui的不确定状态认知结果误差熵定义为:
| $ R_i^\omega i{, _s} = {\rm{ }} - {\rm{log}}{_2}\left( {1 - \frac{{|\mathit{\pmb{D}}_i^\omega {, _s}|}}{{|\mathit{\pmb{D}}_i^\omega {, _s}| + |\mathit{\pmb{D}}_i^\omega {, _s}|}}, } \right) $ | (14) |
式中, |·|表示矩阵中全体元素的绝对值之和。熵值越大表示当前尺度下不确定状态认知结果的可信度越低, 需要增加尺度在更细节特征空间对状态进行再认知。
4.2 绝缘子状态反馈认知调节机制为了模仿人类根据认知结果可信度自优化调节特征空间模式, 借鉴马尔科夫决策过程[19]定义如下性能指标J :
| $ {J_\omega } = \sum\limits_{i = 1}^Z {R_i^w{, _s}/{d_\omega }} {\rm{ }}, 1{\rm{ }} \le \omega \le {\omega _{max}}, $ | (15) |
式中:Ri, sω, /dw表示在第ω次反馈认知中, 测试图像基于深度s的得分, d (d<1)是代价因子。基于Jω, 新增的尺度Δs可定义如下:
| $ \Delta s{\rm{ }} = o({J_\omega }) = {\rm{ }}\tau \frac{{{e^{lJ\omega /Z}} - e{ - ^{lJ\omega /Z}}}}{{{e^{lJ\omega /Z}} + {e^{ - lJ\omega /Z}}}}, \tau > 1, l > 1。$ | (16) |
希望所输出的认知结果具有高可信度。若测试图像相邻两次认知的性能指标差异Jω-Jω+1 < χsta, 则认为不确定认知结果具有高可信度可以输出。否则基于式(16)给出尺度增加策略, 提取更细节的绝缘子图像特征并重构SCN, 交替优化训练新增堆叠神经网络权值, 以获取下一次反馈认知的不确定认知结果。
5 实验结果 5.1 实验数据为了表明本文算法的可行性和有效性, 选取了7 000幅航拍绝缘子图像, 其中随机选取5 600幅航拍图像作为训练集, 剩余1 400幅航拍图像作为测试集, 每幅图像的分辨率为4 288×2 848。SCN中φj和bj的取值范围λ从{0.5, 1, 5, 10, 30, 50, 100}中自动获取, uL={1=10-j}j=47, L的最大值为1 000, SCN的参数组合独立运行10次, 以获取最优的参数配置。所有实验的运行条件设置为CPU i7-8700K, 16G内存和GTX1080Ti显卡。
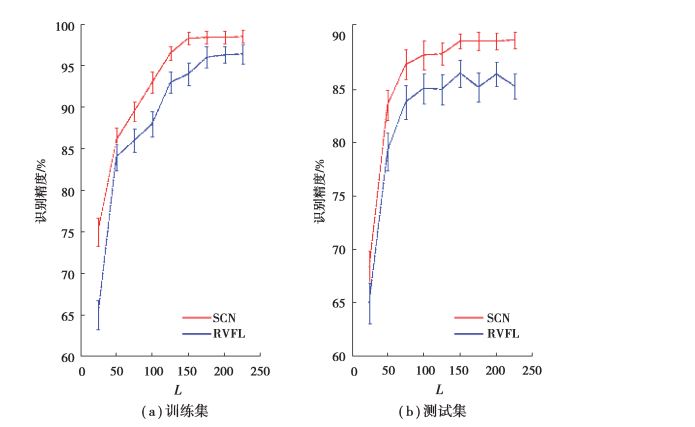
5.2 实验结果在尺度等级s =1的条件下, 图 5给出了当采用不同隐含层节点个数L时, 绝缘子图像训练集和测试集认知精度10次独立实验的均值和标准差变化曲线。可以看出图 5中每个参数点处, SCN的认知精度均优于RVFL, 并随着L不断放大后, 此现象依然存在。L的增加使得认知精度单调递增, 并在L超过150后快速稳定收敛, 表明SCN采用不同的随机基函数, 建立了输入绝缘子图像多尺度特征空间与输出状态之间的非线性关系。
|
图 5 不同隐含层节点个数L条件下的SCN与RVFL认知精度比较 Fig. 5 Cognitive accuracy comparison between SCN and RVFL with different hidden layer node number L |
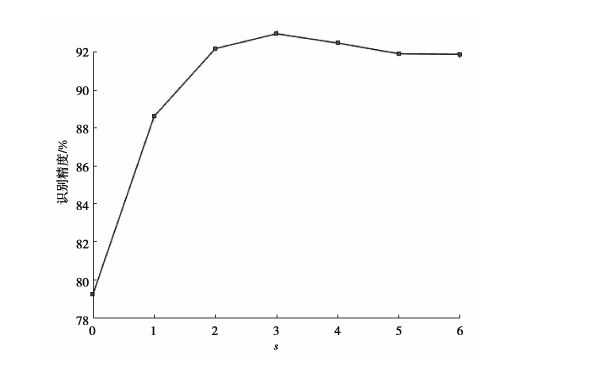
在某次采样实验中, 图 6给出了测试样本集的认知精度关于不同尺度等级s的建模性能, 其中每个点均基于最优SCN参数组合。如图 6所示, s不断增大使得绝缘子状态的认知精度先递增后平稳下降, 这一现象的原因是由于随着网络结构的层层堆叠, 可以引入更细节特征表征输入。然而, 当尺度达到一定的等级后, 所增加的计算量和冗余信息可能会恶化认知性能。不同绝缘子图像具有不同的特征适用度。特别地, s =0表示无堆叠网络, 即开环VGG认知系统, 此时测试样本中约有78%样本的认知结果具有高可信度被正确认知, 剩余22%的测试样本, 通过反馈认知机制增加尺度等级并重构SCN, 约14%的样本在再认知过程中正确输出。
|
图 6 绝缘子状态认知精度vs.尺度等级s Fig. 6 Insulator state cognitive accuracyvs. scale level s |
本文模型的性能与其他深层网络进行了比较, 包括R-CNN[20]、FCAN[21]、PA-CNN[22]、DVAN[16]、VGG-19, 以及具有1级尺度和2级尺度的本文方法。500次实验的平均认知精度和每幅图像的平均认知时间如表 1所示。可以看出, 本文方法的平均识别精度为92.94%, 较其他深层网络模型提高了1% ~13%, 并较尺度较浅的网络模型提高了0.8% ~4.0%。这是由于在深层神经网络的基础上, 通过堆叠细尺度网络架构提取输入图像的多尺度特征空间, 基于SCN构建具有强泛化能力的分类准则, 并采用反馈机制调节尺度等级, 获取低可信度样本的更细节特征以再认知。
| 表 1 不同深层神经网络认知性能的比较 Table 1 Comparison of cognition performance among various deep neural networks |
此外, 为了验证SCN的有效性, 本文方法结合softmax、RVFL、SVM和KNN等多个分类器分别进行了测试。采用相同的绝缘子图像集作为输入, RVFL和SVM的核函数选择高斯函数, 核函数的参数为{24, …, 24 }, 损失参数为{212, …, 2-2 }; KNN的最近邻个数为3。从表 2可以看出, SCN为了使得学习模型具有非线性映射关系的万局逼近能力, 通过在自适应区间内, 根据输出误差约束条件设置输入层与隐含层之间的参数, 以生成新隐含层节点的随机基函数, 使得随机参数设置方法与建模数据关联, 因此较其他分类器具有更好的性能。
| 表 2 不同分类器性能的比较 Table 2 Performance comparison among various classifiers |
探讨了一种基于注意力机制的绝缘子状态反馈认知方法的可行性和有效性。首先, 构建自适应尺度堆叠的卷积神经网络架构提取预处理绝缘子图像多尺度特征。其次, 基于具有万局逼近能力的SCN构建绝缘子图像分类准则。然后, 构建分类和排序损失函数优化注意力网络。最后, 模仿人工巡检模式, 定义广义误差熵性能指标实时评测绝缘子图像不确定状态认知结果可信度, 基于反馈认知机制调节尺度等级, 获取更细节特征空间并重构分类准则以反馈再认知绝缘子图像状态。
| [1] |
Chen K L, Guo Y, Ma X Y. Contactless voltage sensor for overhead transmission lines[J]. IET Generation, Transmission & Distribution, 2018, 12(4): 957-966. |
| [2] |
袁琦. 高压输电线路设计控制要点探讨与对策[J]. 电工技术, 2019(20): 75-76, 78. YUAN Qi. Discussion and countermeasures on design control points of high voltage transmission lines[J]. Electric Engineering, 2019(20): 75-76, 78. (in Chinese) |
| [3] |
Mogi M, Kawamura M, Yoshimi R, et al. A magnetic heterostructure of topological insulators as a candidate for an axioninsulator[J]. Nature Materials, 2017, 16(5): 516-521. DOI:10.1038/nmat4855 |
| [4] |
Du C H, van der Sar T, Zhou T X, et al. Control and local measurement of the spin chemical potential in a magnetic insulator[J]. Science, 2017, 357(6347): 195-198. DOI:10.1126/science.aak9611 |
| [5] |
Zhao Z B, Liu N. The recognition and localization of insulators adopting SURF and IFS based on correlation coefficient[J]. Optik, 2014, 125(20): 6049-6052. DOI:10.1016/j.ijleo.2014.06.094 |
| [6] |
Zhang G N, Liu Z G, Han Y. Automatic recognition for catenary insulators of high-speed railway based on contourlet transform and Chan-Vese model[J]. Optik-International Journal for Light and Electron Optics, 2016, 127(1): 215-221. DOI:10.1016/j.ijleo.2015.10.049 |
| [7] |
Alkali A H, Saatchi R, Elphick H, et al. Thermal image processing for real-time non-contact respiration rate monitoring[J]. IET Circuits, Devices & Systems, 2017, 11(2): 142-148. |
| [8] |
Abeed M A, Biswas A K, Al-Rashid M M, et al. Image processing with dipole-coupled nanomagnets:noise suppression and edge enhancement detection[J]. IEEE Transactions on Electron Devices, 2017, 64(5): 2417-2424. DOI:10.1109/TED.2017.2679604 |
| [9] |
Tan S X, Shen Z X. Hybrid problem-based learning in digital image processing:a case study[J]. IEEE Transactions on Education, 2018, 61(2): 127-135. DOI:10.1109/TE.2017.2766155 |
| [10] |
Wang H, Feng Y M, Sa Y, et al. Pattern recognition and classification of two cancer cell lines by diffraction imaging at multiple pixel distances[J]. Pattern Recognition, 2017, 61: 234-244. DOI:10.1016/j.patcog.2016.07.035 |
| [11] |
Harding S M, Benci J L, Irianto J, et al. Mitotic progression following DNA damage enables pattern recognition within micronuclei[J]. Nature, 2017, 548(7668): 466-470. DOI:10.1038/nature23470 |
| [12] |
Zhang X P, Xiong H K, Zhou W G, et al. Picking deep filter responses for fine-grained image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 27-30, 2016, Las Vegas, NV, USA. IEEE, 2016.
|
| [13] |
Lin T Y, RoyChowdhury A, Maji S. Bilinear CNN models for fine-grained visual recognition[C]//2015 IEEE International Conference on Computer Vision (ICCV), December 7-13, 2015, Santiago, Chile. IEEE, 2015.
|
| [14] |
Zeng X X, Zhang Y, Wang X D, et al. Fine-grained image retrieval via piecewise cross entropy loss[J]. Image and Vision Computing, 2020, 93: 103820. DOI:10.1016/j.imavis.2019.10.006 |
| [15] |
Qi L, Lu X Q, Li X L. Exploiting spatial relation for fine-grained image classification[J]. Pattern Recognition, 2019, 91: 47-55. DOI:10.1016/j.patcog.2019.02.007 |
| [16] |
Zhao B, Wu X, Feng J S, et al. Diversified visual attention networks for fine-grained object classification[J]. IEEE Transactions on Multimedia, 2017, 19(6): 1245-1256. DOI:10.1109/TMM.2017.2648498 |
| [17] |
Wang D H, Li M. Stochastic configuration networks:fundamentals and algorithms[J]. IEEE Transactions on Cybernetics, 2017, 47(10): 3466-3479. DOI:10.1109/TCYB.2017.2734043 |
| [18] |
Girshick R. Fast R-CNN[C/OL]//2015 IEEE International Conference on Computer Vision (ICCV), December 7-13, 2015, Santiago, Chile. IEEE, 2016[2019-12-01]. https://ieeexplore.ieee.org/document/7410526?arnumber=7410526. DOI: 10.1109/ICCV.2015.169.
|
| [19] |
Buongiorno J, Zhou M. Multicriteria forest decisionmaking under risk with goal-programming Markov decision process models[J]. Forest Science, 2017, 63(5): 474-484. |
| [20] |
Girshick R, Donahue J, Darrell T, et al. Rich feature hierarchies for accurate object detection and semantic segmentation[C]//2014 IEEE Conference on Computer Vision and Pattern Recognition, June 23-28, 2014, Columbus, OH, USA. IEEE, 2014.
|
| [21] |
Liu X, Xia T, Wang J, et al. Fully convolutional attention localization networks: efficient attention localization for fine-grained recognition[EB/OL]. (2017-03-21)[2019-12-01]. https://arxiv.org/abs/1603.06765.
|
| [22] |
Krause J, Jin H, Yang J, et al. Fine-grained recognition without part annotations[C/OL]//2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 7-12, 2015, Boston, MA, USA. IEEE, 2015: 5546-5555.[2019-12-01]. https://ieeexplore.ieee.org/document/7299194?arnumber=7299194, DOI: 10.1109/CVPR.2015.7299194,2015.
|
 2020, Vol. 43
2020, Vol. 43


