1b. 重庆大学 机械传动国家重点实验室, 重庆 400044;
2. 哈尔滨工业大学 理学院, 深圳 518055
1b. State Key Laboratory of Mechanical Transmissions, Chongqing University, Chongqing 400044, P. R. China;
2. School of Science, Harbin Institute of Technology, Shenzhen 518055, P. R. China
工程材料的综合性能与航空航天、新能源汽车、集成电路、机械工程、建筑工程等高新技术和民生产业的发展密切相关,材料中存在的杂质或者夹杂往往会改变其宏微观力学性能,从而影响工程结构和零部件的可靠性及使用寿命。Mura[1]将诸如热膨胀、相变、塑性应变和初始应变等非弹性形变统称为本征应变,基体材料中包含的具有本征应变的子区域则称为夹杂。夹杂问题的研究可广泛应用于多个物理力学领域。如热失效是半导体研发中重点关注的问题,芯片在封装测试过程中由于材料热膨胀系数的不匹配会导致芯片出现翘曲[2]、分层失效[3]等现象而影响集成电路的性能。合金在熔炼过程中通常会析出夹杂物[4],而夹杂物的存在有时也可以提高材料的力学性能,例如在面心立方结构FeCoNiCr高熵合金中加入Ti和Al,产生的纳米级共格析出相能够显著增强合金强度[5]。
工程材料中夹杂的形状通常是不规则的,其弹性场的解析解往往不易求解,对于一些特定形状的夹杂,国内外力学工作者已经进行了大量深入的研究。夹杂问题的突破性工作是始于Eshelby[6]对全空间椭球形夹杂的弹性场的研究,发现在均匀本征应变作用下椭球内部的弹性场是均匀分布的,还开创性地提出了等效夹杂方法。Chiu[7]利用伽辽金矢量法给出了全空间长方体夹杂的位移梯度的三重傅里叶积分表达式,进一步可以根据几何方程和胡克定律求出应变场和应力场,随后又基于镜像法研究了半空间长方体夹杂的应力场和表面位移场[8],半空间夹杂问题相对来说更具有工程实际意义,而由于涉及到自由表面的影响,求解过程更加复杂。
对于平面问题,Chiu[9]利用傅里叶变换法,得到了全平面矩形夹杂在平面应力情况下应力场的表达式。Hu[10]将三维半空间退化到平面应变的情况,推导了半平面矩形热夹杂外场的应力场。Ru[11]利用保角变换和解析延拓的方法得到了全平面和半平面任意形状夹杂的解析解。Jin等[12]基于矩形夹杂解[9]推导了平面夹杂问题的应力格林函数,利用格林函数将应力内外场统一表示成面积积分的形式,由于量子线与基体的晶格错配可以用平面应变条件下的静水夹杂模型等效,还指出了其方法在量子线结构中的应用,对于均匀分布的本征应变夹杂问题,可以利用格林定理将应力场转化成围道积分。Jin等[13-14]基于全空间椭球夹杂的结果,通过三维退化的方法,推导了全平面椭圆形夹杂的应力场、应变场和位移场。Li等[15]利用格林函数法推导了平面任意多边形夹杂的位移解,并可将其应用于线性分布本征应变的夹杂问题,与经典的Eshelby椭球夹杂[6]不同,多边形夹杂的内外场位移解可以表示成统一的形式。
笔者利用半空间长方体夹杂解,通过对其一个维度无限延展的极限算法,给出了半无限平面含矩形夹杂的全场位移、应力解,并引入相应的记号方法,将影响系数和响应原函数之间的关系表达成更加直观简洁的形式。针对半平面问题中的任意形状夹杂,可以借助矩形基本单元将其离散-叠加来进行数值求解。以多边形夹杂和圆形夹杂为例,将本文数值解与有限元软件计算结果进行对比,验证了本文方法的正确性。
1 记号方法在平面夹杂问题中,为了求解任意形状夹杂所产生的弹性场,通常可以将任意形状的夹杂离散成大小均匀的矩形单元,通过叠加每个矩形单元所产生的弹性场得到最终的夹杂解。半平面夹杂解可以从三维半空间夹杂问题退化得到,对于半空间问题中夹杂所引起的位移场和应力场可以采用镜像法或直接通过使用势函数和伽辽金矢量法求得[16]。
| $ {u_i}(\mathit{\boldsymbol{x}}) = - \frac{1}{{8{\rm{ \mathit{ π} }}(1 - \nu )}}\int_\mathit{\Omega } {{{\mathit{\underline{\boldsymbol U}} }_i}} \left[ {{\varepsilon ^*}} \right]{\rm{d}}{\mathit{\boldsymbol{x}}^\prime }, $ | (1) |
| $ {\sigma _{ij}}(\mathit{\boldsymbol{x}}) = \left\{ {\begin{array}{*{20}{l}} { - \frac{\mu }{{4{\rm{ \mathit{ π} }}(1 - \nu )}}\int_\mathit{\Omega } {{{\mathit{\boldsymbol{ \boldsymbol{\underline \varTheta} }} }_{ij}}} \left[ {{\varepsilon ^*}} \right]{\rm{d}}{\mathit{\boldsymbol{x}}^\prime }, }&{\mathit{\boldsymbol{x}} \notin \mathit{\Omega }, }\\ { - \frac{\mu }{{4{\rm{ \mathit{ π} }}(1 - \nu )}}\int_\mathit{\Omega } {{{\mathit{\boldsymbol{ \boldsymbol{\underline \varTheta} }} }_{ij}}} \left[ {{\varepsilon ^*}} \right]{\rm{d}}{\mathit{\boldsymbol{x}}^\prime } - \lambda \varepsilon _{kk}^*{\delta _{ij}} - 2\mu \varepsilon _{ij}^*, }&{\mathit{\boldsymbol{x}} \in \mathit{\Omega }。} \end{array}} \right. $ | (2) |
式中:λ和μ为拉梅常数;ν为泊松比;δij为Kronecker符号;本征应变
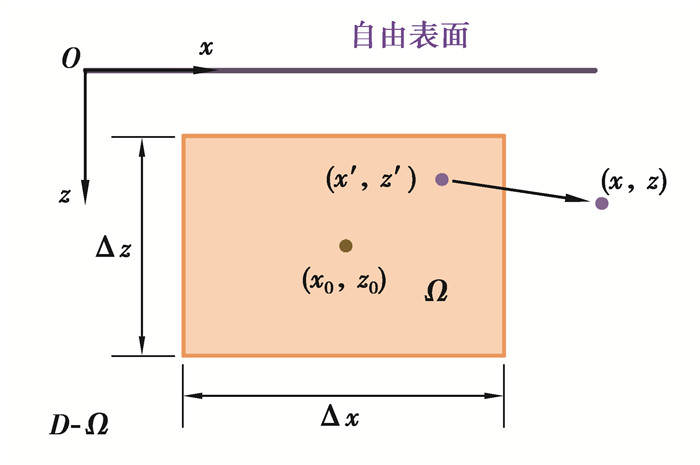
如果令长方体夹杂沿y轴方向的长度趋于无穷大,则三维空间问题就会退化成平面应变问题。夹杂问题可以从激励-响应的角度去理解,通过引入矩形夹杂基本单元解的记号方法,可以将复杂的叠加求和运算表示成更加直观、简洁的形式[17]。假设在半无限大平面D中存在一个矩形夹杂Ω,夹杂内部分布着均匀的本征应变
|
图 1 半平面矩形夹杂示意图 Fig. 1 Schematic diagram of rectangular inclusion in half-planev |
与全平面对应的卷积积分可以表示为
| $ g_1=\int_{z_0-\frac{\Delta z}{2}}^{z_0+\frac{\Delta z}{2}} \int_{x_0-\frac{\Delta x}{2}}^{x_0+\frac{\Delta x}{2}} G_1\left(x-x^{\prime}, z-z^{\prime}\right) \mathrm{d} x^{\prime} \mathrm{d} z^{\prime}。$ | (3) |
与镜像项对应的卷积-自相关积分可以表示成
| $ g_2=\int_{z_0-\frac{\Delta z}{2}}^{z_0+\frac{\Delta z}{2}} \int_{x_0-\frac{\Delta x}{2}}^{x_0+\frac{\Delta x}{2}} G_2\left(x-x^{\prime}, z+z^{\prime}\right) \mathrm{d} x^{\prime} \mathrm{d} z^{\prime} 。$ | (4) |
考虑如下变量代换
| $ \xi_1=x-x^{\prime}, \xi_3= \begin{cases}z-z^{\prime}, & \text { 与全平面相关项, } \\ z+z^{\prime}, & \text { 与镜像项相关项。}\end{cases} $ | (5) |
使用变量代换,并交换积分上下限后,式(3)(4)可以写成如下表达形式
| $ {g_1} = \int_{{z_1}}^{{z_2}} {\int_{{x_1}}^{{x_2}} {{G_1}\left( {{\xi _1}, {\xi _3}} \right){\rm{d}}{\xi _1}{\rm{d}}{\xi _3}} } , $ | (6) |
| $ g_2=\int_{\widehat{z_1}}^{\widehat{z_2}} \int_{x_1}^{x_2} G_2\left(\xi_1, \xi_3\right) \mathrm{d} \xi_1 \mathrm{~d} \xi_{3 \circ} $ | (7) |
其中
| $ \left\{\begin{array}{l} x_1=x-x_0-\Delta x / 2, \\ x_2=x-x_0+\Delta x / 2, \\ z_1=z-z_0-\Delta z / 2, \\ z_2=z-z_0+\Delta z / 2, \\ \hat{z}_1=z+z_0-\Delta z / 2, \\ \hat{z_2}=z+z_0+\Delta z / 2 。\end{array}\right. $ | (8) |
如果格林函数
| $ {g_1} = \sum\limits_{\alpha = 1}^2 {\sum\limits_{\gamma = 1}^2 {{{( - 1)}^{\alpha + \gamma }}} } {\mathit{\Gamma }_1}\left( {{x_\alpha }, {z_\gamma }} \right) = {\mathit{\Gamma }_1}\left( {{x_1}, {z_1}} \right) - {\mathit{\Gamma }_1}\left( {{x_1}, {z_2}} \right) - {\mathit{\Gamma }_1}\left( {{x_2}, {z_1}} \right) + {\mathit{\Gamma }_1}\left( {{x_2}, {z_2}} \right)。$ | (9) |
上述式子中括号里的变量分别表示矩形的4个角点指向响应点的向量的分量,根据金晓清等[17]所引入的记号方法,式(9)可以写成
| $ {g_1} = {\mathit{\Gamma }_1}(x, z)\mid \left[ {{x_0}, {z_0};\Delta x, \Delta z} \right]。$ | (10) |
同样地,如果
| $ {g_2} = \sum\limits_{\alpha = 1}^2 {\sum\limits_{\gamma = 1}^2 {{{( - 1)}^{\alpha + \gamma }}} } {\mathit{\Gamma }_2}\left( {{x_\alpha },\widehat {{z_\gamma }}} \right) = {\mathit{\Gamma }_2}\left( {{x_1},\widehat {{z_1}}} \right) - {\mathit{\Gamma }_2}\left( {{x_1},\widehat {{z_2}}} \right) - {\mathit{\Gamma }_2}\left( {{x_2},\widehat {{z_1}}} \right) + {\mathit{\Gamma }_2}\left( {{x_2},\widehat {{z_2}}} \right)。$ | (11) |
采用上述记号方法,与镜像夹杂相关的响应解g2可以表示成如下形式
| $ {g_2} = {\mathit{\Gamma }_2}(x, z)\mid \left[ {{x_0}, - {z_0};\Delta x, \Delta z} \right]。$ | (12) |
式(10)和式(12)中所采用的记号方法包含了计算场点(x, z)处响应所需的全部必要信息,即矩形激励区域的中心坐标(x0, z0),矩形边长Δx,Δz,响应解g1和g2分别是由场点坐标、矩形中点坐标、矩形边长所组成的4个积分上下限在响应原函数
采用数值离散方法求解任意形状夹杂问题时一般可以通过将计算域离散成大小均匀的矩形单元,然后叠加每个矩形夹杂单元所产生弹性场求出最终的数值解,因此有必要研究单个矩形夹杂产生的位移、应力场,也即半平面夹杂问题的基本单元解。
半平面夹杂问题中位移场的基本单元解的矩阵表达形式如下:
| $ \left[\begin{array}{l} u_1 \\ u_3 \end{array}\right]=\left[\begin{array}{llll} W_{111} & W_{122} & W_{133} & W_{113} \\ W_{311} & W_{322} & W_{333} & W_{313} \end{array}\right]\left[\begin{array}{c} \varepsilon_{11}^* \\ \varepsilon_{22}^* \\ \varepsilon_{33}^* \\ 2 \varepsilon_{13}^* \end{array}\right], $ | (13) |
其中,位移影响系数Wikl与位移响应原函数wikl之间的关系可以用引入的记号方法表示为
| $ \begin{array}{c} {W_{ikl}} = W_{ikl}^{(0)} + W_{ikl}^{(1)} + zW_{ikl}^{(2)} + {z^2}W_{ikl}^{(3)} = \\ - \frac{1}{{8{\rm{ \mathit{ π} }}(1 - \nu )}}\left\{ {w_{ikl}^{(0)}\left| {\left[ {{x_0}, {z_0};\Delta x, \Delta z} \right] + \left[ {w_{ikl}^{(1)} + zw_{ikl}^{(2)} + {z^2}w_{ikl}^{(3)}} \right]} \right|\left[ {{x_0}, - {z_0};\Delta x, \Delta z} \right]} \right\}。\end{array} $ | (14) |
式(14)中
| $ \left\{\begin{array}{l} w_{111}^{(0)}=-2(3-2 \nu) \xi_3 \ln r-4(1-\nu) \xi_1 \arctan \frac{\xi_3}{\xi_1}, \\ w_{122}^{(0)}=-4 \nu\left(\xi_3 \ln r+\xi_1 \arctan \frac{\xi_3}{\xi_1}\right), \\ w_{133}^{(0)}=2(1-2 \nu) \xi_3 \ln r-4 \nu \xi_1 \arctan \frac{\xi_3}{\xi_1}, \\ w_{113}^{(0)}=-2(1-2 \nu) \xi_1 \ln r-4(1-\nu) \xi_3 \arctan \frac{\xi_1}{\xi_3}, \\ w_{311}^{(0)}=2(1-2 \nu) \xi_1 \ln r-4 \nu \xi_3 \arctan \frac{\xi_1}{\xi_3}, \\ w_{322}^{(0)}=-4 \nu\left(\xi_1 \ln r+\xi_3 \arctan \frac{\xi_1}{\xi_3}\right), \\ w_{333}^{(0)}=-2(3-2 \nu) \xi_1 \ln r-4(1-\nu) \xi_3 \arctan \frac{\xi_1}{\xi_3}, \\ w_{313}^{(0)}=-2(1-2 \nu) \xi_3 \ln r-4(1-\nu) \xi_1 \arctan \frac{\xi_3}{\xi_1} 。\end{array}\right. $ | (15) |
其中
与三维半空间夹杂问题类似,在二维半平面基体中夹杂所引起的弹性场问题中,与全平面相关的积分核是关于x,z的卷积,另外3项与镜像夹杂相关的积分核是关于x的卷积和z的自相关。式(14)中的
| $ \left\{\begin{array}{l} w_{111}^{(1)}=-2(5-6 \nu) \xi_3 \ln r-4(1-\nu) \xi_1 \arctan \frac{\xi_3}{\xi_1}, \\ w_{122}^{(1)}=-4(3-4 \nu) \nu\left(\xi_3 \ln r+\xi_1 \arctan \frac{\xi_3}{\xi_1}\right), \\ w_{133}^{(1)}=-2(1-2 \nu) \xi_3 \ln r-4(2-3 \nu) \xi_1 \arctan \frac{\xi_3}{\xi_1}, \\ w_{113}^{(1)}=-2(1-2 \nu) \xi_1 \ln r+4(1-\nu) \xi_3 \arctan \frac{\xi_1}{\xi_3}, \\ w_{311}^{(1)}=2(1-2 \nu) \xi_1 \ln r+4(2-3 \nu) \xi_3 \arctan \frac{\xi_1}{\xi_3}, \\ w_{322}^{(1)}=4(3-4 \nu) \nu\left(\xi_1 \ln r+\xi_3 \arctan \frac{\xi_1}{\xi_3}\right), \\ w_{333}^{(1)}=2(5-6 \nu) \xi_1 \ln r+4(1-\nu) \xi_3 \arctan \frac{\xi_1}{\xi_3}, \\ w_{313}^{(1)}=2(1-2 \nu) \xi_3 \ln r-4(1-\nu) \xi_1 \arctan \frac{\xi_3}{\xi_1} 。\end{array}\right. $ | (16) |
| $ \begin{cases}w_{111}^{(2)}=4(1-2 \nu) \ln r+\frac{4 \xi_1^2}{r^2}, & w_{122}^{(2)}=-8 \nu \ln r, \\ w_{133}^{(2)}=-4(3-2 \nu) \ln r+\frac{4 \xi_3^2}{r^2}, & w_{113}^{(2)}=8(1-\nu) \arctan \frac{\xi_3}{\xi_1}-\frac{4 \xi_1 \xi_3}{r^2}, \\ w_{311}^{(2)}=8(1-\nu) \arctan \frac{\xi_3}{\xi_1}+\frac{4 \xi_1 \xi_3}{r^2}, & w_{322}^{(2)}=-8 \nu \arctan \frac{\xi_1}{\xi_3}, \\ w_{333}^{(2)}=-8 \nu \arctan \frac{\xi_1}{\xi_3}-\frac{4 \xi_1 \xi_3}{r^2}, & w_{313}^{(2)}=-4(1-2 \nu) \ln r-\frac{4 \xi_3^2}{r^2}。\end{cases} $ | (17) |
| $ \left\{ {\begin{array}{*{20}{l}} {w_{111}^{(3)} = w_{313}^{(3)} = \frac{{4{\xi _3}}}{{{r^2}}}, }&{w_{133}^{(3)} = - \frac{{4{\xi _3}}}{{{r^2}}}, }&{w_{113}^{(3)} = w_{333}^{(3)} = \frac{{4{\xi _1}}}{{{r^2}}}, }\\ {w_{311}^{(3)} = - \frac{{4{\xi _1}}}{{{r^2}}}, }&{w_{122}^{(3)} = w_{322}^{(3)} = 0。}&{} \end{array}} \right. $ | (18) |
半平面夹杂问题中应力的基本单元解的矩阵形式可以表示为
| $ \left[\begin{array}{l} \sigma_{11} \\ \sigma_{22} \\ \sigma_{33} \\ \sigma_{13} \end{array}\right]=\left[\begin{array}{llll} T_{1111} & T_{1122} & T_{1133} & T_{1113} \\ T_{2211} & T_{2222} & T_{2233} & T_{2213} \\ T_{3311} & T_{3322} & T_{3333} & T_{3313} \\ T_{1311} & T_{1322} & T_{1333} & T_{1313} \end{array}\right]\left[\begin{array}{c} \varepsilon_{11}^* \\ \varepsilon_{22}^* \\ \varepsilon_{33}^* \\ 2 \varepsilon_{13}^* \end{array}\right] 。$ | (19) |
影响系数Tijkl与应力响应原函数tijkl之间的关系可以表示为
| $ \begin{array}{C} {T_{ijkl}} = T_{ijkl}^{(0)} + T_{ijkl}^{(1)} + zT_{ijkl}^{(2)} + {z^2}T_{ijkl}^{(3)} = \\ - \frac{E}{{8{\rm{ \mathit{ π} }}\left( {1 - {\nu ^2}} \right)}}\left\{ {t_{ijkl}^{(0)}\left| {\left[ {{x_0}, {z_0};\Delta x, \Delta z} \right] + \left[ {t_{ijkl}^{(1)} + zt_{ijkl}^{(2)} + {z^2}t_{ijkl}^{(3)}} \right]} \right|\left[ {{x_0}, - {z_0};\Delta x, \Delta z} \right]} \right\}, \end{array} $ | (20) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {t_{1111}^{(0)} = 4\arctan \frac{{{\xi _1}}}{{{\xi _3}}} - \frac{{2{\xi _1}{\xi _3}}}{{{r^2}}},}&{t_{1133}^{(0)} = t_{3311}^{(0)} = t_{1313}^{(0)} = \frac{{2{\xi _1}{\xi _3}}}{{{r^2}}},}&{t_{1113}^{(0)} = t_{1311}^{(0)} = - 2\ln r + \frac{{2\xi _1^2}}{{{r^2}}},}\\ {t_{3333}^{(0)} = 4\arctan \frac{{{\xi _3}}}{{{\xi _1}}} - \frac{{2{\xi _1}{\xi _3}}}{{{r^2}}},}&{t_{3313}^{(0)} = t_{1333}^{(0)} = - 2\ln r + \frac{{2\xi _3^2}}{{{r^2}}},}&{t_{1122}^{(0)} = t_{2211}^{(0)} = 4\nu \arctan \frac{{{\xi _1}}}{{{\xi _3}}},}\\ {t_{2233}^{(0)} = t_{3322}^{(0)} = 4\nu \arctan \frac{{{\xi _3}}}{{{\xi _1}}},}&{t_{2222}^{(0)} = 4\left( {\arctan \frac{{{\xi _1}}}{{{\xi _3}}} + \arctan \frac{{{\xi _3}}}{{{\xi _1}}}} \right),}&{t_{1322}^{(0)} = t_{2213}^{(0)} = - 4\nu \ln r。} \end{array}} \right. $ | (21) |
| $ \left\{ {\begin{array}{*{20}{l}} {t_{1111}^{(1)} = - 4\arctan \frac{{{\xi _3}}}{{{\xi _1}}} - \frac{{6{\xi _1}{\xi _3}}}{{{r^2}}},}&{t_{1122}^{(1)} = - 12\nu \arctan \frac{{{\xi _3}}}{{{\xi _1}}},}&{t_{1133}^{(1)} = - 8\arctan \frac{{{\xi _3}}}{{{\xi _1}}} + \frac{{6{\xi _1}{\xi _3}}}{{{r^2}}},}\\ {t_{1113}^{(1)} = - 2\ln r - \frac{{6\xi _1^2}}{{{r^2}}},}&{t_{2211}^{(1)} = - 4\nu \arctan \frac{{{\xi _3}}}{{{\xi _1}}} - \frac{{8\nu {\xi _1}{\xi _3}}}{{{r^2}}},}&{t_{2222}^{(1)} = - 16{\nu ^2}\arctan \frac{{{\xi _3}}}{{{\xi _1}}},}\\ {t_{2233}^{(1)} = - 12\nu \arctan \frac{{{\xi _3}}}{{{\xi _1}}} - \frac{{8\nu {\xi _1}{\xi _3}}}{{{r^2}}},}&{t_{2213}^{(1)} = - 4\nu \ln r + \frac{{8\nu \xi _1^2}}{{{r^2}}},}&{t_{3311}^{(1)} = - \frac{{2{\xi _1}{\xi _3}}}{{{r^2}}},}\\ {t_{3322}^{(1)} = - 4\nu \arctan \frac{{{\xi _3}}}{{{\xi _1}}},}&{t_{3333}^{(1)} = - 2\arctan \frac{{{\xi _3}}}{{{\xi _1}}} + \frac{{2{\xi _1}{\xi _3}}}{{{r^2}}},}&{t_{3313}^{(1)} = - 2\ln r - \frac{{2\xi _1^2}}{{{r^2}}},}\\ {t_{1311}^{(1)} = - 2\ln r + \frac{{2\xi _1^2}}{{{r^2}}},}&{t_{1322}^{(1)} = - 4\nu \ln r,}&{t_{1333}^{(1)} = - 2\ln r - \frac{{2\xi _1^2}}{{{r^2}}},}\\ {t_{1313}^{(1)} = - \frac{{2{\xi _1}{\xi _3}}}{{{r^2}}}。}&{}&{} \end{array}} \right. $ | (22) |
| $ \left\{ {\begin{array}{*{20}{l}} {t_{1111}^{(2)} = \frac{{12{\xi _1}}}{{{r^2}}} - \frac{{8\xi _1^3}}{{{r^4}}}, }&{t_{1122}^{(2)} = - \frac{{8\nu {\xi _1}}}{{{r^2}}}, }&{t_{1133}^{(2)} = - \frac{{12{\xi _1}}}{{{r^2}}} - \frac{{8{\xi _1}\xi _3^2}}{{{r^4}}}, }\\ {t_{1113}^{(2)} = - \frac{{12{\xi _3}}}{{{r^2}}} - \frac{{8\xi _1^2{\xi _3}}}{{{r^4}}}, }&{t_{2211}^{(2)} = \frac{{8\nu {\xi _1}}}{{{r^2}}}, }&{t_{2222}^{(2)} = 0, }\\ {t_{2233}^{(2)} = - \frac{{8\nu {\xi _1}}}{{{r^2}}}, }&{t_{3311}^{(2)} = \frac{{4{\xi _1}}}{{{r^2}}} - \frac{{8\xi _3^2{\xi _1}}}{{{r^4}}}, }&{t_{2213}^{(2)} = - \frac{{8\nu {\xi _3}}}{{{r^2}}}, }\\ {t_{3322}^{(2)} = \frac{{8\nu {\xi _1}}}{{{r^2}}}, }&{t_{3333}^{(2)} = \frac{{4{\xi _1}}}{{{r^2}}} + \frac{{8{\xi _1}\xi _3^2}}{{{r^4}}}, }&{t_{3313}^{(2)} = - \frac{{4{\xi _3}}}{{{r^2}}} + \frac{{8\xi _3^3}}{{{r^4}}}, }\\ {t_{1311}^{(2)} = \frac{{4{\xi _3}}}{{{r^2}}} - \frac{{8\xi _1^2{\xi _3}}}{{{r^4}}}, }&{t_{1322}^{(2)} = - \frac{{8\nu {\xi _3}}}{{{r^2}}}, }&{t_{1333}^{(2)} = - \frac{{4{\xi _3}}}{{{r^2}}} - \frac{{8\xi _3^3}}{{{r^4}}}, }\\ {t_{1313}^{(2)} = \frac{{4{\xi _1}}}{{{r^2}}} + \frac{{8{\xi _1}\xi _3^2}}{{{r^4}}}。}&{}&{} \end{array}} \right. $ | (23) |
| $ \begin{cases}t_{1111}^{(3)}=t_{3333}^{(3)}=t_{1313}^{(3)}=-\frac{8 \xi_1 \xi_3}{r^4}, & t_{1133}^{(3)}=t_{3311}^{(3)}=\frac{8 \xi_1 \xi_3}{r^4}, \\ t_{1113}^{(3)}=t_{1333}^{(3)}=\frac{4}{r^2}-\frac{8 \xi_1^2}{r^4}, & t_{3313}^{(3)}=t_{1311}^{(3)}=-\frac{4}{r^2}+\frac{8 \xi_1^2}{r^4}, \\ t_{1122}^{(3)}=t_{2211}^{(3)}=t_{2222}^{(3)}=t_{2233}^{(3)}=t_{2213}^{(3)}=t_{3322}^{(3)}=t_{1322}^{(3)}=0 。\end{cases} $ | (24) |
根据平面应变条件,可以验证由面内本征应变
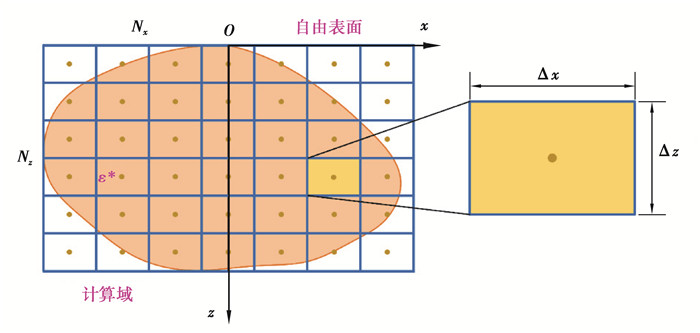
对于半平面夹杂问题,采用有限元法计算时需要在一个半无限域上进行网格离散,也即计算域尺寸需要远远大于夹杂尺寸,而且还需在夹杂边界周围细化网格才能满足计算精度。基于上一节中求得半平面夹杂的基本单元解,只需将包含任意形状夹杂的矩形有限计算域离散成Nx×Nz个大小均匀的矩形网格单元,计算域的中心为(x0, z0),边长分别为2a,2b。激励场单元和响应场单元中点的位置编号分别定义为(m′, n′)和(m, n)。为了避免在运算过程中进行坐标变换增加计算量,矩形单元的边分别平行于对应的坐标轴,边长分别为Δx,Δz,如图 2所示。
|
图 2 半平面任意形状夹杂矩形单元离散示意图 Fig. 2 Schematic diagram of discrete rectangular element of arbitrarily shaped inclusion in half-plane |
以位移解为例,通过叠加离散后的矩形单元解,就可以得到任意形状夹杂位移场的数值解,如式(25)所示。应力解可以通过同样的离散方法求得。
| $ \begin{array}{c} {u_i}(m, n) = \sum\limits_{{n^\prime } = 1}^{{N_z}} {\sum\limits_{{m^\prime } = 1}^{{N_x}} {W_{ikl}^{(0)}} } \left( {m - {m^\prime }, n - {n^\prime }} \right)\varepsilon _{kl}^*\left( {{m^\prime } + {n^\prime }} \right) + \\ \sum\limits_{{n^\prime } = 1}^{{N_z}} {\sum\limits_{{m^\prime } = 1}^{{N_x}} {W_{ikl}^{(1)}} } \left( {m - {m^\prime }, n - {n^\prime }} \right)\varepsilon _{kl}^*\left( {{m^\prime } + {n^\prime }} \right) + \\ z\sum\limits_{{n^\prime } = 1}^{{N_z}} {\sum\limits_{{m^\prime } = 1}^{{N_x}} {W_{ikl}^{(2)}} } \left( {m - {m^\prime }, n - {n^\prime }} \right)\varepsilon _{kl}^*\left( {{m^\prime } + {n^\prime }} \right) + \\ {z^2}\sum\limits_{{n^\prime } = 1}^{{N_z}} {\sum\limits_{{m^\prime } = 1}^{{N_x}} {W_{ikl}^{(3)}} } \left( {m - {m^\prime }, n - {n^\prime }} \right)\varepsilon _{kl}^*\left( {{m^\prime } + {n^\prime }} \right)。\end{array} $ | (25) |
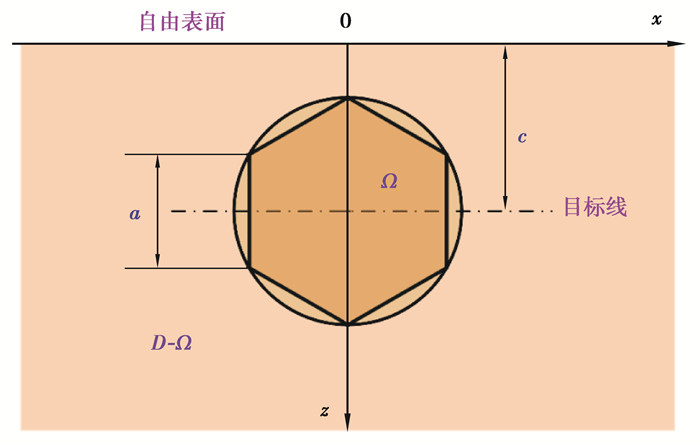
通过矩形基本单元离散任意形状夹杂,再叠加求和通常需要进行大量的数值计算,可结合快速傅里叶变换算法进行加速计算[16, 18]。为了验证半平面夹杂基本单元解的正确性,以多边形夹杂和圆形夹杂为例,如图 3所示,考虑在无限大的半平面基体材料中存在着一个正六边形/圆形夹杂,夹杂的中心位于(0, c),边长/半径为a,本征应变为
|
图 3 半平面六边形/圆形夹杂模型示意图 Fig. 3 Schematic diagram of hexagon/circular inclusion model in half-plane |
| 表 1 半平面六边形/圆形夹杂模型参数 Table 1 Parameters of hexagon/circular inclusion model in half plane |
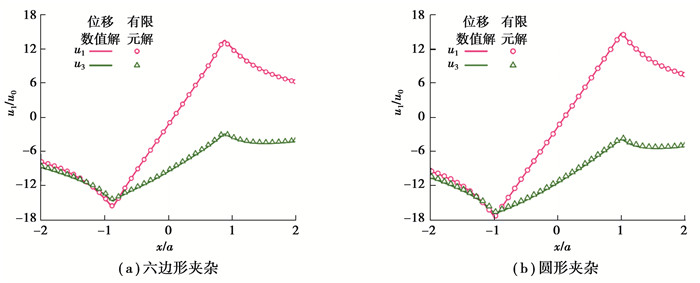
利用FORTRAN编程得到的数值解和ABAQUS有限元解进行对比验证,目标线的起始点坐标分别为(-2, 2)和(2, 2)。为了消除量纲对数据对比带来的影响,需要对应力和输出点位置进行无量纲化处理,即
|
图 4 位移数值解和有限元解对比结果 Fig. 4 Verification of the displacement numerical solutions with FEM results |
|
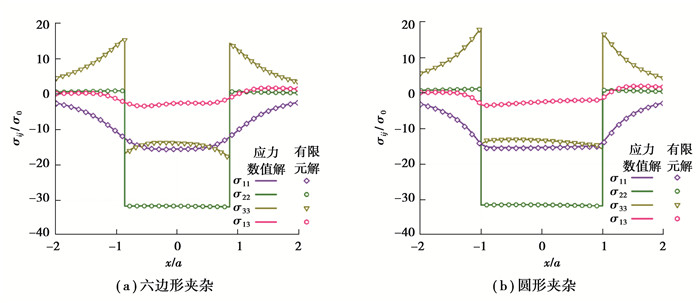
图 5 应力数值解和有限元解对比结果 Fig. 5 Verification of the stress numerical solutions with FEM results |
1) 通过将长方体夹杂的一个维度无限延展的极限算法,推导了平面应变问题中二维半平面矩形夹杂的位移、应力场的基本单元解。与经典的Eshelby椭球夹杂解相比,矩形夹杂内外弹性场的解析解可以写成统一的形式。进一步还可以通过平面应变和平面应力的转化关系,将文中提出的基本单元解应用到平面应力情况。
2) 以位移解为例,通过矩形单元离散任意形状夹杂,推导了半平面任意形状夹杂位移场的数值解形式,将提出的基本单元解应用于求解半平面夹杂问题弹性场的数值解。
3) 以半平面正六边形和圆形夹杂为例,将本文中的数值方法与有限元软件仿真结果进行对比,验证了所推导的矩形基本单元解及数值算法的正确性。
| [1] |
Mura T. Micromechanics of defects in solids[M]. Second, revised ed. Dordrecht: Martinus Nijhoff Publishers, 1987.
|
| [2] |
Cheng H C, Tai L C, Liu Y C. Theoretical and experimental investigation of warpage evolution of flip chip package on packaging during fabrication[J]. Materials, 2021, 14(17): 4816. DOI:10.3390/ma14174816 |
| [3] |
黄涛, 廖秋慧, 吴文云, 等. 叠层芯片结构QFN封装导电胶分层失效行为分析[J]. 电子元件与材料, 2020, 39(9): 97-104. Huang T, Liao Q H, Wu W Y, et al. Analysis of delamination failure behavior of QFN packaging conductive adhesive with laminated chip structure[J]. Electronic Components and Materials, 2020, 39(9): 97-104. (in Chinese) |
| [4] |
朱诚意, 罗小燕, 李光强, 等. 无取向硅钢中含镁夹杂物的形成机理分析[J]. 重庆大学学报, 2018, 41(8): 34-43. Zhu C Y, Luo X Y, Li G Q, et al. Formation mechanism analysis on magnesium-bearing inclusions in non-oriented silicon steels[J]. Journal of Chongqing University, 2018, 41(8): 34-43. (in Chinese) |
| [5] |
He J Y, Wang H, Huang H L, et al. A precipitation-hardened high-entropy alloy with outstanding tensile properties[J]. Acta Materialia, 2016, 102: 187-196. DOI:10.1016/j.actamat.2015.08.076 |
| [6] |
Eshelby J D. The determination of the elastic field of an ellipsoidal inclusion, and related problems[J]. Proceedings of the Royal Society of London Series A-Mathematical and Physical Sciences, 1957, 241(1226): 376-396. |
| [7] |
Chiu Y P. On the stress field due to initial strains in a cuboid surrounded by an infinite elastic space[J]. Journal of Applied Mechanics, 1977, 44(4): 587-590. DOI:10.1115/1.3424140 |
| [8] |
Chiu Y P. On the stress field and surface deformation in a half space with a cuboidal zone in which initial strains are uniform[J]. Journal of Applied Mechanics, 1978, 45(2): 302-306. DOI:10.1115/1.3424292 |
| [9] |
Chiu Y P. On the internal stresses in a half plane and a layer containing localized inelastic strains or inclusions[J]. Journal of Applied Mechanics, 1980, 47(2): 313-318. DOI:10.1115/1.3153661 |
| [10] |
Hu S M. Stress from a parallelepipedic thermal inclusion in a semispace[J]. Journal of Applied Physics, 1989, 66(6): 2741-2743. DOI:10.1063/1.344194 |
| [11] |
Ru C Q. Analytic solution for Eshelby's problem of an inclusion of arbitrary shape in a plane or half-plane[J]. Journal of Applied Mechanics, 1999, 66(2): 315-523. DOI:10.1115/1.2791051 |
| [12] |
Jin X Q, Keer L M, Wang Q. New Green's function for stress field and a note of its application in quantum-wire structures[J]. International Journal of Solids and Structures, 2009, 46(21): 3788-3798. DOI:10.1016/j.ijsolstr.2009.07.005 |
| [13] |
Jin X Q, Keer L M, Wang Q. A closed-form solution for the Eshelby tensor and the elastic field outside an elliptic cylindrical inclusion[J]. Journal of Applied Mechanics, 2011, 78(3): 031009. DOI:10.1115/1.4003238 |
| [14] |
Jin X Q, Zhang X N, Li P, et al. On the displacement of a two-dimensional Eshelby inclusion of elliptic cylindrical shape[J]. Journal of Applied Mechanics, 2017, 84(7): 074501. DOI:10.1115/1.4036820 |
| [15] |
Li P, Zhang X N, An Y H, et al. Analytical solution for the displacement of a polygonal inclusion with a special application to the case of linear eigenstrain[J]. European Journal of Mechanics - A/Solids, 2020, 84: 104049. DOI:10.1016/j.euromechsol.2020.104049 |
| [16] |
Liu S B, Jin X Q, Wang Z J, et al. Analytical solution for elastic fields caused by eigenstrains in a half-space and numerical implementation based on FFT[J]. International Journal of Plasticity, 2012, 35: 135-154. DOI:10.1016/j.ijplas.2012.03.002 |
| [17] |
金晓清, 牛飞飞, 张睿, 等. 均布激励基本单元解析解的一种记号方法[J]. 上海交通大学学报, 2016, 50(8): 1221-1227. Jin X Q, Niu F F, Zhang R, et al. A notation for elementary solution to uniformly distributed excitation over a rectangular/cuboidal domain[J]. Journal of Shanghai Jiao Tong University, 2016, 50(8): 1221-1227. (in Chinese) |
| [18] |
Sun L L, Wang Q, Zhang M Q, et al. Discrete convolution and FFT method with summation of influence coefficients (DCS-FFT) for three-dimensional contact of inhomogeneous materials[J]. Computational Mechanics, 2020, 65(6): 1509-1529. |
 2022, Vol. 45
2022, Vol. 45


