混合动力汽车(HEV)发展迅速,已逐渐成为未来汽车重要发展方向之一。动力电池作为HEV的主要储能元件,直接影响到HEV的性能。镍氢电池(MH-Ni)是继Cd-Ni电池之后的新一代高能二次电池。由于它具有比能量高、比功率高、寿命长、充电快速、记忆效应不明显、污染少等优点[1],成为HEV的首选电池。镍氢电池组在充、放电过程中会产生大量的热量,如果散热不及时,会导致电池组内部的温度过高和电池组模块之间温度分布不均匀,可充入的电量减少,从而影响电池的性能和寿命[2-4]。为了提高电池性能的可靠性,不仅要求电池组的工作温度保持在临界温度之下,而且要求各单体电池之间的温差控制在一定的范围以内。因此,建立电池温度场分析的理论模型,采用数值模拟技术分析电池在使用条件下的温度分布,进行电池散热性能预测,对提高电池使用性能具有重要的现实意义。
以美国NREL(national renewable energy laboratory)为代表,国外先进的研究机构已开发出MH-Ni电池的热设计软件,其仿真结果直接用于镍氢电池组的设计。进入21世纪,中国才开始将仿真分析应用于MH-Ni电池的研发,对MH-Ni电池进行温度场仿真分析所用软件以Fluent为主。Desikan Bharathan[5]、常国峰等[6]针对不同电池厂商的镍氢电池组进行了电池单位体积或单位面积生热速率恒定的温度场稳态仿真分析,没有进行电池单位体积生热速率随时间变化的温度场瞬态仿真。Yu L J[7]、杨亚联等[8]分别对镍氢电池单体和镍氢电池组进行了温度场瞬态仿真分析,但没有进行汽车行驶工况下镍氢电池的温度场实验,输入的电池单位体积生热速率与整车实际运行工况不符。文中以国内某汽车厂开发的混合动力汽车用镍氢电池组为对象,首先对镍氢电池组进行了流场分析,确定流量分配,然后对镍氢电池组进行了温度场稳态仿真分析,根据分析结果给出了整车温度场试验时传感器的布点方案,最后进行了整车电池温度场试验,并以实验测得数据为边界条件进行了最恶劣工况下镍氢电池组温度场瞬态仿真分析。结果表明:仿真值和实验值吻合度良好,验证了所建模型的正确性;电池组散热性能良好,满足混合动力汽车对动力电池的使用要求。
1 流动与传热的控制方程镍氢电池组通过离心式抽风机进行强制冷却,所涉及的物理模型主要是流动和热交换,在流动与传热的过程中遵循质量守恒、动量守恒及能量守恒定律。
在三维直角坐标系中,xi、xj、xk为坐标系中i、j、k方向上的分量;流体速度矢量U在3个坐标上的分量分别为ui,uj,uk;压力为p;流体的密度为ρ;时间为t。Fluent中求解能量方程形式为[9]
| $\begin{array}{l} \quad \quad \frac{\partial }{{\partial t}}\left( {\rho E} \right) + \frac{\partial }{{\partial {x_i}}}\left[ {{u_i}\left( {\rho E + p} \right)} \right] = \\ \frac{\partial }{{\partial {x_i}}}\left[ {{k_{{\rm{eff}}}}\frac{{\partial T}}{{\partial {x_i}}} - \sum\limits_{{j^\prime }} {{h_{{j^\prime }}}} {J_{{j^\prime }}} + {u_j}{{({\tau _{ij}})}_{{\rm{eff}}}}} \right] + {S_{\rm{h}}}, \end{array}$ | (1) |
式中:E为流体微团的总能;T为时间;keff有效导热系数;hj′为组分j′的焓;Jj′是组分j′的扩散通量;(τij)eff是偏应力张量。右边前3项分别为导热项,组分扩散项和粘性耗散项。Sh为包括化学反应热和其他体积热源的源项。
标准k-ε两方程模型,包括湍流脉动动能方程(也称k方程)和耗散率ε的控制方程[10]为:
| $\begin{array}{l} \rho \frac{{\partial k}}{{\partial t}} + \rho {u_j}\frac{{\partial k}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\eta + \frac{{{\eta _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + \\ \quad \quad {\eta _t}\frac{{\partial {u_i}}}{{\partial {x_j}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \rho \varepsilon , \end{array}$ | (2) |
| $\begin{array}{l} \rho \frac{{\partial \varepsilon }}{{\partial t}} + \rho {u_k}\frac{{\partial \varepsilon }}{{\partial {x_k}}} = \frac{\partial }{{\partial {x_k}}}\left[ {\left( {\eta + \frac{{{\eta _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_k}}}} \right] + \\ \quad \frac{{{c_1}\varepsilon }}{k}{\eta _t}\frac{{\partial {u_i}}}{{\partial {x_j}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - {c_2}\rho \frac{{{\varepsilon ^2}}}{k}。\end{array}$ | (3) |
湍流粘性系数ηt的方程为
| ${\eta _t} = {c_\mu }\rho {k^2}/\varepsilon 。$ | (4) |
采用k-ε模型求解湍流对流换热问题时,控制方程包括质量方程、动量方程、能量方程及k、ε方程与ηt方程,共引入3个经验系数(c1,c2,cu)及3个常数(σk,σε,σT),在近年发表的文献中,这6个经验常数的取值已经比较一致,其值如表 1所示。
文中所研究的电池组温度场仿真分析,主要涉及电池组和箱体的对流换热,流动为湍流。标准k-ε两方程模型有较高的稳定性、经济性和计算精度,是目前工程中解决湍流问题主要的计算模型。文中采用标准k-ε两方程模型进行数值模拟,计算时所需参数设置如表 1所示。
2 镍氢电池的生热模型热量的计算是建模求解电池温度场的基础。工程应用中准确获得电池单位体积生热速率q的表达式比较困难,目前主要由理论和实验2种方法获得[13]。Bernadi等[14]基于电池内部物质发热均匀的假设给出了一种电池生热的模型,Nobor Sato和Kazuhiko Yagi[15]利用电化学反应原理分析了MH-Ni电池的生热量,根据电化学反应中电子迁移个数与反应生热量之间的关系,得到化学反应生热速率和电池充放电电流之间的关系式。文中即采用此方法计算MH-Ni电池的生热量。
MH-Ni电池的生热因素主要有以下4项:电池化学反应生热、电池极化生热、过充电副反应生热和内阻焦耳热。电池的充电过程分为2个阶段:在没有发生充电副反应之前为第1个阶段,生热量主要来自电池化学反应生热、电池极化生热、内阻焦耳热。其生热量的表达式为
| ${Q_{{\rm{charge1}}}} = 0.547{I_{\rm{c}}} + 3.6I_{\rm{c}}^2{R_t},$ | (5) |
式中:Qcharge1为电池充电第1阶段的生热量,kJ/h;Ic为电池的充电电流,A;Rt为电池内阻和极化内阻之和, Ω。
在发生过充电副反应之后为第2阶段,生热量主要来自电池化学反应生热、电池极化生热、过充电副反应生热、内阻焦耳热。其中大部分的生热量来自于过充电副反应生热。充电末期和过充电时,过充电副反应就开始发生,其生热量为
| ${Q_{{\rm{charge}}}}_2 = 5.334{I_{\rm{c}}} + 3.6I_{\rm{c}}^2{R_t},$ | (6) |
式中,Qcharge2为发生过充电副反应的生热量,kJ/h。
电池放电过程中的生热量主要来自电池化学反应生热、电池极化生热和内阻焦耳热。MH-Ni电池放电时化学反应为吸热反应,所以生热问题不是很严重,其生热量为
| ${Q_{{\rm{discharge}}}} = - 0.547{I_{\rm{d}}} + 3.6I_{\rm{d}}^2{R_t},$ | (7) |
式中:Qdischarge为电池在放电过程中的生热量,kJ/h;Id为电池的放电电流,A。
MH-Ni电池在充放电过程中产生的总热量为
| ${Q_{{\rm{Bat}}}} = {Q_{{\rm{charge1}}}} + {Q_{{\rm{charge2}}}} + {Q_{{\rm{discharge}}}},$ | (8) |
式中QBat为电池在充放电过程中产生的总热量,kJ/h。
在进行镍氢电池组温度场瞬态仿真分析时,利用实验监测得到的电流数据,由公式(5)~(8)可计算出电池组在充放电过程中总生热量,从而得到电池单位体积的生热速率,以此为体积热源的源项,加载到公式(1)的Sh项中。
3 镍氢电池组散热系统仿真分析 3.1 镍氢电池组工作压差的确定文中所研究的HEV电池箱体和DC/DC并联,由同一款离心式抽风机冷却。为了进行电池组温度场分析,先进行并联管路的流场分析,以确定风机的工作点。根据并联管路的压力损失原理,风机工作点处的压差即为所有并联管路的工作压差,从而确定镍氢电池组的工作压差。
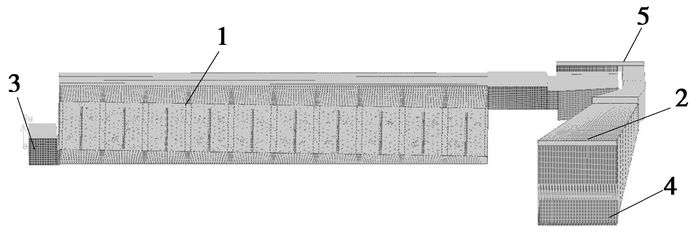
并联管路散热系统的网格模型如图 1所示,网格数目为2 599 348。仿真分析时选取进出风口的压差为边界条件,依次计算不同压差输入时模型的流量,仿真分析结果所得系统并联管路压力损失如表 2所示。
|
图 1 并联管路散热系统网络模型 注:1.电池组冷却流道;2.DC/DC冷却流道;3.电池组冷却进风口;4.DC/DC冷却进风口;5.散热系统出风口 |
| 表 2 并联管路压力损失表 |
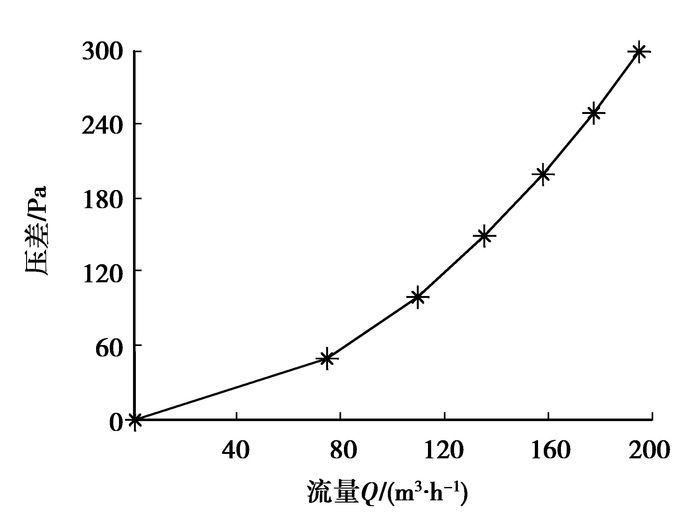
由并联管路的压力损失规律可得散热系统的管路性能曲线,如图 2所示。
|
图 2 散热系统管路性能曲线 |
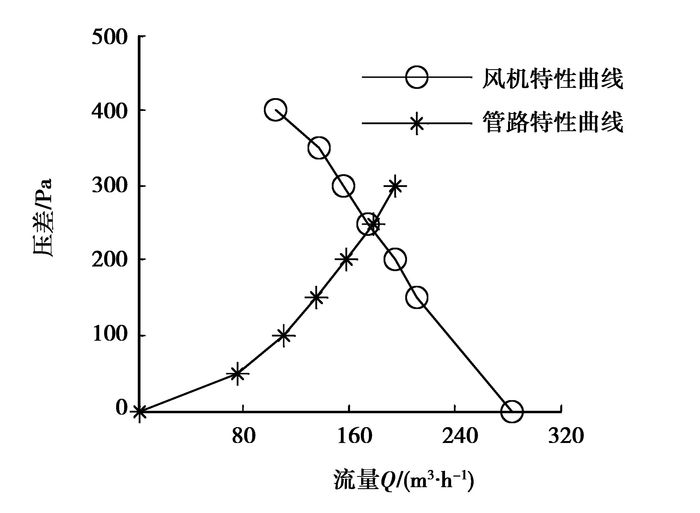
风机性能曲线由风机厂商提供,根据风机的自动平衡原理,风机的性能曲线与散热系统管路的性能曲线按同一比例绘制在同一坐标图中,2条曲线的交点即为风机工作点,如图 3所示。
|
图 3 风机工作点的确定 |
可知,所选用离心式风机在该散热系统中以额定功率工作时,风机进出风口的压差为245 Pa,此压差即为电池组流场进出风口的压差,从而确定电池组温度场仿真时的边界条件。
3.2 镍氢电池组温度场稳态仿真分析 3.2.1 模型建立与边界条件所研究的HEV车用镍氢电池组包括12个模块,每个模块由10个单体电池组成,实物如图 4所示。

|
图 4 镍氢电池组结构图 |
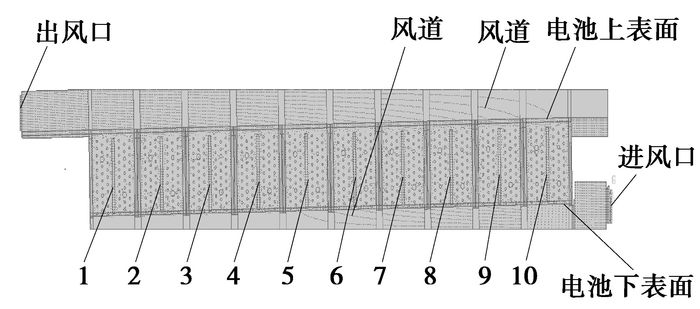
12个模块具有对称性,相当于并联连接,由于在Gambit建模时可以采用对称面作为边界条件,且每个模块具有对称性,取1个模块的一半进行仿真。所建网格模型如图 5所示,模型网格数目为1 374 547,图中1~10为电池编号。
|
图 5 镍氢电池组网格模型 |
边界条件的设定:进出风口为压力边界条件,压差为245 Pa,进风口及环境温度为313 K,对称面采用对称边界条件,电池单位体积的生热速率为78 125 W/m3,模型采用标准k-ε两方程模型,参数选取如表 1所示,在数值计算中采用SIMPEC算法[16],以提高计算的收敛性,缩短计算时间。各介质物性参数如表 3所示。
| 表 3 介质物性参数 |
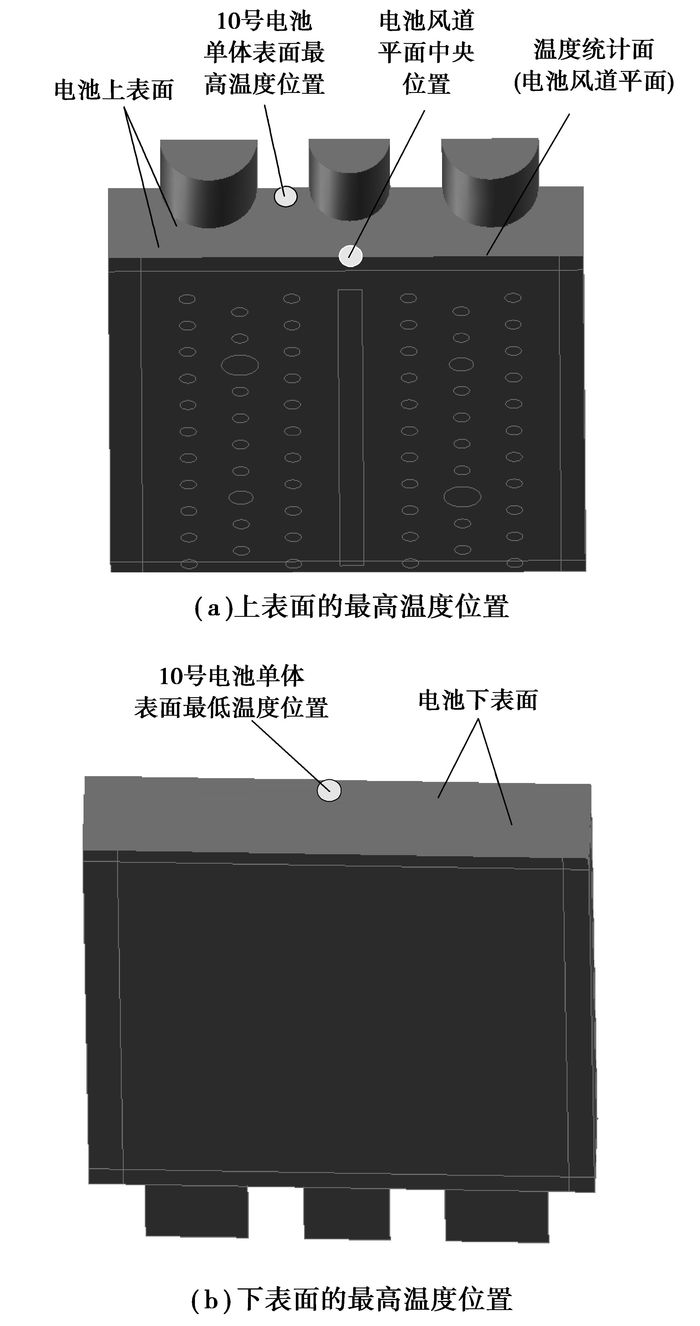
温度的统计面选择在与电池上表面平齐的风道所在平面,以10号电池为例,具体位置如图 6(a)所示,利用Fluent软件分别统计1~10号电池统计面的平均温度。
|
图 6 10号电池温度统计面及监测点 |
镍氢电池组温度场稳态仿真分析结果如图 7所示。对于1~10号电池风道平面的平均温度而言,6号电池统计面的平均温度最高,为50.2 ℃,1号电池统计面的平均温度最低,为48.6 ℃;每个电池单体的表面温度可通过在Fluent软件中查看每个电池单体表面的温度云图,分别找出1~10号每个电池单体表面的最高温度和最低温度所在位置。由仿真结果可知,1~10每个电池单体表面的最高温度均位于电池的上表面,1~10每个电池单体表面的最低温度均位于电池的下表面,以10号电池为例,其电池单体表面最高温度和最低温度的位置如图 6(a)、6(b)所示。

|
图 7 电池组温度云图 |
实验在某企业技术中心的整车性能实验室环境舱中进行,室内试验系统主要包括环境仓、底盘测功机、鼓风机、数据测试系统。数据测试系统主要由HEV、T型热电耦传感器、日本横河数据采集控制器MW100、德国Vector公司的CANcas工具、计算机等组成。
T型热电耦类型为铜-康铜传感器,测量温度范围为-200~100 ℃,精度为±1.5 ℃。横河数据采集控制器有5个模块,每个模块有10个采集通道,共有50个采集通道。
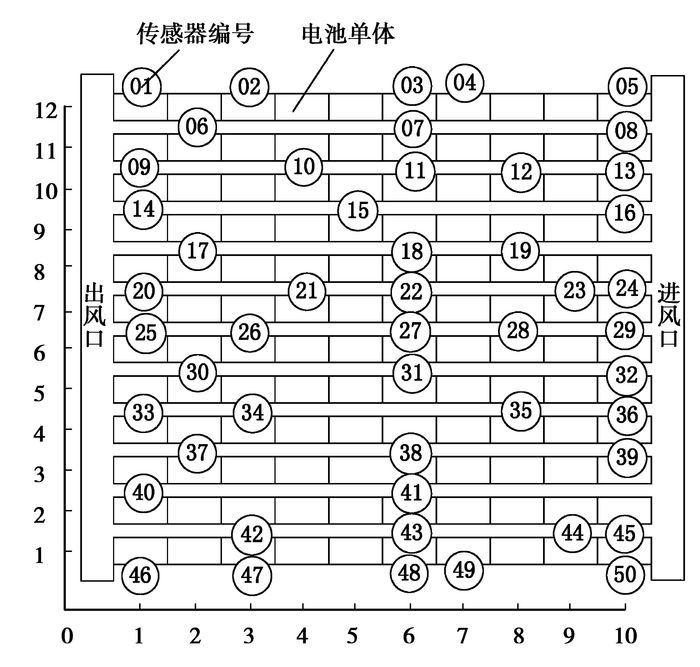
4.2 温度传感器布点方案温度传感器布置于电池温度统计面(风道平面)的中央位置,如图 6(a)所示。根据镍氢电池组稳态仿真结果,6号电池统计面的平均温度最高,1号电池统计面的平均温度最低,故6号和1号电池统计面处的温度应重点监测,传感器布点方案如图 8所示,图中横坐标代表电池编号,纵坐标代表电池模块编号。
|
图 8 电池组上表面传感器布点方案 |
对HEV车用镍氢电池组温度场进行车载实验时,实验环境温度为40±2 ℃,相对湿度为50%±5%,日照强度为1 000±50 W/m2。实验共进行5个工况,按时间先后顺序依次为6%爬坡工况、10%爬坡工况、怠速工况、城市堵车工况及急加速急减速工况,每一个工况都包括暖车阶段和工况阶段,5个工况之间无时间间隔。其中急加速急减速工况为最恶劣工况,文中重点对此工况进行研究,实验规范如表 4所示。
| 表 4 暖车及预处理阶段实验工况 |
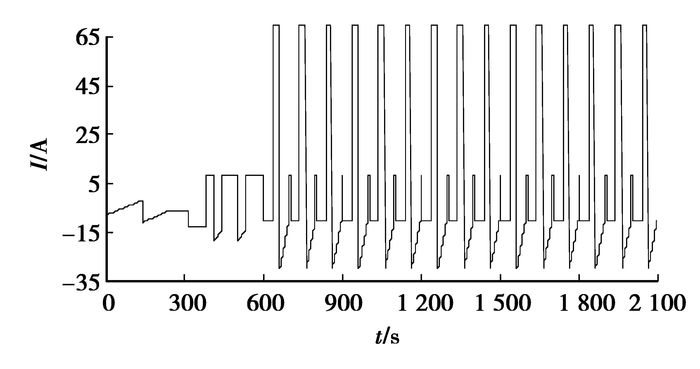
实验时利用德国Vector公司生产的CANcas工具读取CAN总线上的电池充放电电压、电流及SOC值。在急加速急减速工况中,将所记录的充放电电流进行数据拟合,所得拟合曲线如图 9所示。
|
图 9 电池组充放电电流拟合曲线 |
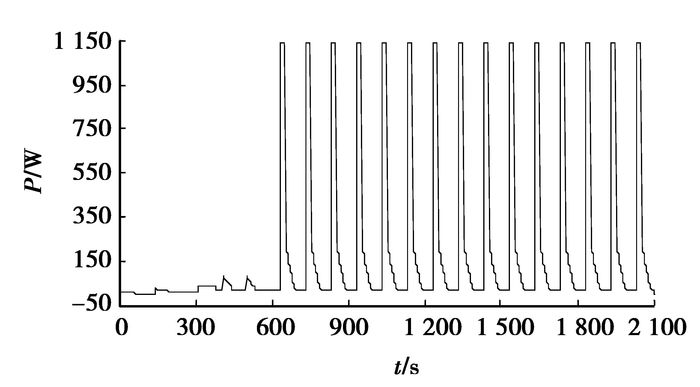
对镍氢电池组进行瞬态仿真分析时,电池充放电放时产生的热量由公式(5)~(8)计算得到,图 10为经拟合后电池组的发热功率图,在Fluent中编写用户自定义函数,以计算的单位体积生热速率为源项在加载到公式(1)中Sh处。
|
图 10 电池组发热功率图 |
电池组温度场瞬态仿真分析的边界条件与稳态仿真分析的边界条件基本一致,唯一的不同是电池单位体积发热速率的取值。稳态仿真分析时其值是恒定的,为78 125 W/m3,而瞬态仿真分析时其值是瞬态变化的,大小由公式(5)~(8)计算得到,如图 10所示。
对瞬态问题进行数值模拟,时间步长设置为5 s。在1~10号电池风道平面中央位置、每个电池单体表面最高温度位置和最低温度位置设置监视器,统计这些点处的温度值。以10号电池为例,具体位置如图 6(a)、6(b)所示。
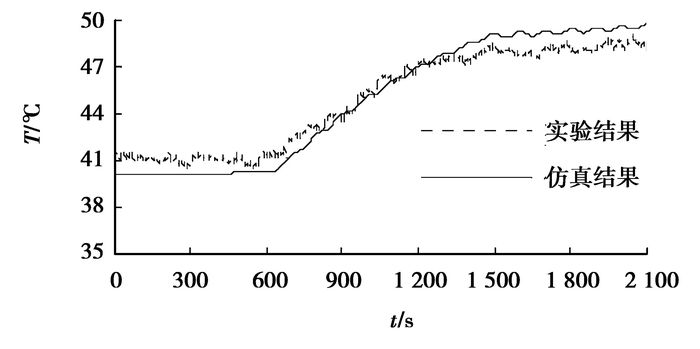
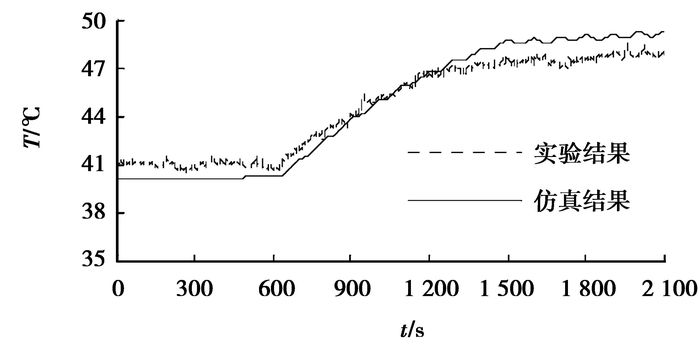
4.5 仿真与实验结果对比分析利用Fluent软件对建立的镍氢电池组进行瞬态数值模拟,由仿真结果可知,在1~10号电池风道平面中央位置的监测点中,6号和1号电池监测点为温度最高与最低点,且位置不随时间变化。文中取图 8中27号传感器测得温度与6号电池风道平面中央位置温度监测点的瞬态仿真结果作对比分析,结果如图 11所示;取图 8中25号传感器测得温度与1号电池风道平面中央位置温度监测点的瞬态仿真结果作对比分析,结果如图 12所示。
|
图 11 6号电池风道平面温度监测点实验结果和仿真结果 |
|
图 12 1号电池风道平面温度监测点实验结果和仿真结果 |
从图 11、12可以看出,仿真值和实验值较为吻合,呈现出大致相同的变化趋势。同时,暖车阶段(0~600 s)实验值比仿真值偏高,主要原因为:在进行急加速急减速工况时,由于前一个实验工况(城市堵车工况)刚完成,产生的电池发热量没有及时散出,以致实验环境温度高于40 ℃,而文中仿真分析时选取的环境温度为40 ℃,从而导致温度的实验值比仿真值偏高;工况阶段(600~2 165 s)实验值比仿真值偏低,这是由于在使用公式(5)~(8)计算电池单位体积的发热速率时,电池内阻由电池厂商提供,其值取电池充放电过程中的最大值,所以仿真分析时输入的电池发热速率比实验时的发热速率大,从而导致温度的实验值比仿真值偏低。
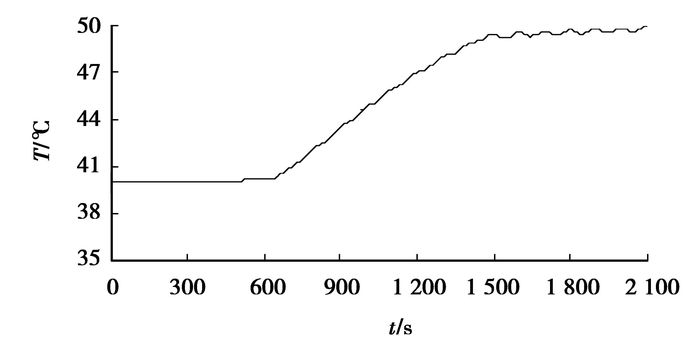
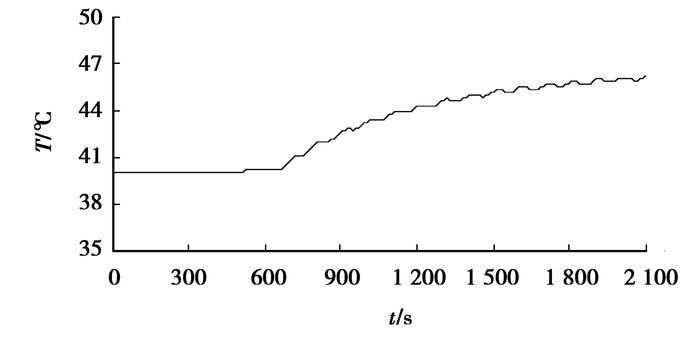
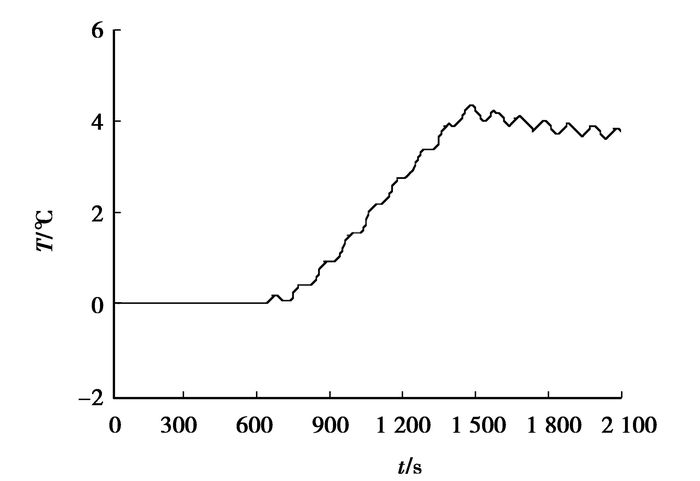
就每个电池单体表面温度而言,在1~10号每个电池单体表面最高温度位置的监测点中,10号电池单体表面监测点的温度最高,且位置不随时间变化,仿真结果如图 13所示;在1~10号每个电池单体表面最低温度位置的监测点中,10号单体电池表面监测点的温度最低,且位置不随时间变化,仿真结果如图 14所示,电池表面最高温度为49.97 ℃。电池组最大温差(10号电池表面最高温度位置监测点与10号电池表面最低温度位置监测点的温差)如图 15所示,最大温差为4.3 ℃。散热强度和散热均衡性良好,满足HEV对动力电池的使用要求。
|
图 13 10号电池表面最高温度监测点仿真结果 |
|
图 14 10号电池表面最低温度监测点仿真结果 |
|
图 15 电池组最大温差 |
1) 建立了镍氢电池组散热系统模型,采用计算流体力学方法对散热系统进行流场分析,确定电池组和DC/DC的流量分配,并对电池组进行了温度场稳态分析,根据仿真结果给出了实验时传感器的布点方案。
2) 进行了汽车行驶工况下镍氢电池组的温度场实验,以实验监测数据作为输入条件,对电池组进行瞬态仿真分析。仿真值与实验值吻合良好,表明利用Fluent软件对镍氢电池组温度场进行仿真分析,能较好地反映电池组的温度分布情况。
3) 电池表面最高温度为49.97 ℃,最大温差为4.37 ℃,表明散热系统散热性能良好,满足HEV对动力电池的使用要求。
| [1] |
朱鹏, 于立军, 杨立, 等.
镍氢电池的数值模拟[J]. 微计算机信息, 2008, 24(1/2): 173–175.
ZHU Peng, YU Lijun, YANG Li, et al. Numerical simulation of nickel hydrogen battery[J]. Control & Automation, 2008, 24(1/2): 173–175. (in Chinese) |
| [2] | Shi J Z, Wu F, Hu D Z, et al. The influence of hydrogen intercalation on inner pressure of Ni/MH battery during fast charge[J]. Journal of Power Sources, 2006, 161(1): 692–701. DOI:10.1016/j.jpowsour.2006.04.076 |
| [3] | Buerlein P, Antonius C, Lffler J, et al. Progress in high-power nickel-metal hydride batteries[J]. Journal of Power Sources, 2008, 176(2): 547–554. DOI:10.1016/j.jpowsour.2007.08.052 |
| [4] | Li D H, Kai Y, Shi C. Thermal behavior of overcharged nickel/metal hydride batteries[J]. Journal of Power Sources, 2008, 184(2): 622–626. DOI:10.1016/j.jpowsour.2008.03.059 |
| [5] | Bharathan D, Pesaran A, Vlahinos A, et al. Improving battery design with electro-thermal modeling[C]//Proceedings of the 2005 IEEE Conference on Vehicle Power and Propulsion, September 7-9, 2005, Chicago, USA. Piscataway:IEEE Press, 2005:368-375. |
| [6] |
常国峰, 陈磊涛, 许思传, 等.
镍氢电池热管理系统结构优化设计[J]. 同济大学学报:自然科学版, 2009, 37(11): 1518–1520.
CHANG Guofeng, CHENG Leitao, XU Sichuan, et al. Structural optimization design of nickelhydrogen battery thermal management system[J]. Journal of Tongji University:Natural Science, 2009, 37(11): 1518–1520. (in Chinese) |
| [7] | Yu L J, Qin M J, Zhu P, et al. Numerical simulation and optimization of nickel-hydrogen batteries[J]. Journal of Power Sources, 2008, 179(2): 848–853. DOI:10.1016/j.jpowsour.2007.12.126 |
| [8] |
杨亚联, 张昕, 李隆键, 等.
基于CFD的混合动力车用镍氢电池散热系统研究[J]. 汽车工程, 2009, 31(3): 214–219.
YANG Yalian, ZHANG Xin, LI Longjian, et al. A study on the cooling system of Ni/MH batteries for hybrid electric vehicle based on CFD analysis[J]. Automotive Engineering, 2009, 31(3): 214–219. (in Chinese) |
| [9] | 温正, 石良辰, 任毅如. FLUENT流体计算应用教程[M]. 北京: 清华大学出版社, 2009. |
| [10] | 陶文铨. 数值传热学[M]. 2版. 陕西: 西安交通大学出版社, 2008. |
| [11] | Jafari A, Tynjälä T, Mousavi S M, et al. Simulation of heat transfer in a ferrofluid using computational fluid dynamics technique[J]. International Journal of Heat and Fluid Flow, 2008, 29(4): 1197–1202. DOI:10.1016/j.ijheatfluidflow.2008.01.007 |
| [12] |
杨亚联, 陈方元, 秦大同, 等.
混合动力汽车用DC-DC和IPU散热结构优化[J]. 重庆大学学报, 2010, 33(7): 1–6.
YAN Yalian, CHEN Fangyuan, QIN Datong, et al. Heat dissipation optimization of DC-DC and IPU for hybrid electric vehicle[J]. Journal of Chongqing University, 2010, 33(7): 1–6. DOI:10.11835/j.issn.1000-582X.2010.07.001 (in Chinese) |
| [13] |
杨凯, 李大贺, 陈实, 等.
电动汽车动力电池的热效应模型[J]. 北京理工大学学报, 2008, 28(9): 782–785.
YANG Kai, LI Dahe, CHEN Shi, et al. Thermal model of batteries for electrical vehicle[J]. Journal of Beijing Institute of Technology, 2008, 28(9): 782–785. (in Chinese) |
| [14] | Bernadi D, Pawlikowski E, Newman J. A general energy balance for battery systems[J]. Journal of the Electrochemical Society, 1985, 132(1): 5–12. DOI:10.1149/1.2113792 |
| [15] | Sato N, Yagi K. Thermal behavior analysis of nickel metal hydride batteries for electric vehicles[J]. JSAE Review, 2000, 21(2): 205–211. DOI:10.1016/S0389-4304(99)00096-X |
| [16] | Darbandi M, Naderi A. Multiblock hybrid grid finite volume method to solve flow in irregular geometries[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 196(1/2/3): 321–336. |
 2013, Vol. 36
2013, Vol. 36

