高炉炼铁过程涉及复杂的化学反应、流动、相变、热量传输、质量传输以及动量传输等现象,并且高炉内部过程由于其高温和封闭性基本不可测量,因此,高炉被认为是冶金领域最复杂的反应器。高炉研究专家和学者一直致力于通过科学的方法了解和表征高炉内的真实情况,在众多的研究方法中,数学模型(如20世纪90年代提出的多流体模型)有其特有的优势。它能够在考虑高炉内化学反应、传热、传质等众多复杂现象的基础上,借助流体商业软件或自编程序通过数学迭代的方法计算和反映高炉内的温度场、速度场、浓度场等重要信息,从而更直观地了解高炉内部情况,数学模型的许多重要成果已经应用在实际的生产过程中[1]。Yagi等[2]曾经建立和完善了多流体高炉数学模型,并应用建立的模型对高炉流程进行了详细的研究,取得很多开创性的成果。
另外,高炉炼铁是一个高耗能、高污染的过程并且高炉炼铁产生大量的CO2,带来巨大的资源和环境压力。氧气高炉炼铁技术通过对目前的普通高炉进行改造,从而达到炼铁过程节能减排、提高生产效率的目的。主要的变化有使用全氧或高浓度氧气鼓风代替传统的预热空气鼓风和炉顶煤气经处理后循环返回高炉,它具有高喷煤量、低焦比、高生产率和高煤气品质等突出优点[3]。
氧气高炉炼铁工艺之所以还没有大规模的推广和应用,除制氧成本和CO2脱除成本较高的原因外,还因为炉顶循环煤气加热技术不成熟以及相对于传统高炉氧气高炉炉内状态发生了一系列变化,其中一个最关键的难题就是“上冷下热”。通过实验室还原实验[4]和氧气高炉热化学模型[5]可以了解氧气高炉内矿石还原过程的变化以及氧气高炉的各项宏观参数,但是这些方法都不能用来研究各种参数在氧气高炉内部的具体分布。而通过将多流体高炉数学模型应用于氧气高炉的研究,可以详细地预测和了解氧气高炉内部状况,对流程设计和实际操作提供有益的参考。Nogami和Chu等[6-7]曾经利用建立的多流体高炉数学模型研究了炉顶煤气循环工艺的效果。但是这些研究都只简单阐述了循环煤气条件下高炉的基本特征,对氧气高炉相对于普通高炉各种参数的变化及其规律缺乏细致的研究。笔者旨在通过建立的氧气高炉多流体模型详细对比分析GF-FOBF流程中氧气高炉和普通高炉的差异,从而为氧气高炉的设计和流程开发提供有益的指导。
1 多流体高炉数学模型的建立 1.1 模型涉及的物相和反应模型将高炉内的物质划分为3种状态,其中气体组分划分为气相,固体含铁炉料及焦炭划分为固相,液态渣及铁水划分为液相[8-9]。对于煤粉颗粒,没有处理为单独的一相,而是假设煤粉在风口循环区瞬间燃烧完毕。每一相中都含有相应的物质,各物质具有特定的物性参数。本研究对高炉所涉及的相及物质进行了尽可能地简化,并在此基础上做了一些合理的假设。模型中所涉及的相及物质见表 1。
| 表 1 模型涉及的相及物质 Table 1 Phases and substances involved in the model |
在对高炉内的相及众多物质进行简化的基础上,对炉内发生的反应也进行了简化,只考虑一些主要的反应。表 2列出了模型所考虑的12个化学反应及3个相变。矿石的间接还原反应采用未反应核模型进行计算。
| 表 2 模型涉及的化学反应及相变 Table 2 Chemical reactions and phase transitions involved in the model |
模型中涉及的高炉内多相体系主要包括了气相、固相、液相。高炉的计算区域并不复杂,包括了炉顶料面至炉缸渣铁液面间的区域。高炉的复杂性在于高炉内的化学反应和相间相互作用,其中的化学反应数量众多,而其相间相互作用则包括了气、固、液相间复杂的热量交换及动量交换。基于此考虑,在计算时把每一相的计算分布到不同的计算机节点上,而对计算区域不作分区。
高炉内物料行为遵循质量守恒、动量守恒及能量守恒3个定律。为便于计算机编程及求解,这些守恒定律可以用一个统一的形式来表示,见式(1)。
| $ \frac{\partial \left({{\varepsilon }_{i}}{{\rho }_{i}}\psi \right)}{\partial t}+\text{div}\left({{\varepsilon }_{i}}{{\rho }_{i}}U\psi \right)=\text{div}\left({{\varepsilon }_{i}}{{\Gamma }_{\psi }}\text{grad}\psi \right)+{{S}_{\psi }}, $ | (1) |
式中:εi为高炉中i相体积分数;ρi为i流体密度,kg/m3;U为i流体速度矢量,m/s;ψ为守恒方程通用变量,可以用u,v,w,H等求解;Γψ为守恒方程广义扩散系数;Sψ为守恒方程广义源项。
1.3 相间动量及热量传输模型中,气固、气液、固液相间作用力分别用Ergun公式[10]、Richardson-Zaki公式[11]、和Kozeny-Carmen公式[12]进行计算。同样地,气固、气液、固液相间热交换计算分别采用Ranz-Marshall公式[13]、Mackey-Warner公式[14]和Eckert-Drake公式[15]进行计算。
1.4 模型边界条件和求解策略模型中气、固、液三相的边界条件不尽相同,具体设置如下所述:
1)气相。在高炉风口处,假设喷吹煤粉中固定碳与鼓风中氧气已瞬间反应,且完全生成CO,因此,风口处气体成分及温度设置为煤粉与鼓风反应后气体的组分与温度。在高炉炉顶出口处,气流是充分发展的。
炉墙对于气相是自由滑动边界。炉墙总热损被平均分配给气相及固相。在炉墙附近的网格中,气相能量源项中炉墙热损部分的计算见式(2)。
| $ {{Q}_{\text{g, wall}}}=0.5{{A}_{\text{wall}}}{{h}_{\text{wall}}}\left(\frac{{{T}_{\text{g}}}+{{T}_{\text{s}}}}{2}-{{T}_{\text{wall}}} \right), $ | (2) |
式中:Qg, wall为炉墙气相热损,W;Awall为炉墙面积,m2;hwall为对流换热系数,W/(m2·K);Tg, Ts为炉墙表面气相和固相温度,K;Twall为炉墙温度,K。
2)固相。料面处固相组分及温度按照实际生产参数进行设置。固相出口设置在炉墙的底部,出口处固相流是充分发展的。炉墙及死料面对固相流动有一定的摩擦阻力。固相能量方程中炉墙热损部分的计算见式(3)。
| $ {{Q}_{\text{s, wall}}}=0.5{{A}_{\text{wall}}}{{h}_{\text{wall}}}\left(\frac{{{T}_{\text{g}}}+{{T}_{\text{s}}}}{2}-{{T}_{\text{wall}}} \right), $ | (3) |
式中:Qs, wall为炉墙固相热损,W;其他参数同式(2)。
3)液相。炉墙对于液相是自由滑动边界。液相可以自由穿过高炉下部渣铁界面。
模型求解借助了CFD商用软件PHOENICS[16]。由于气、液、固三相间存在较强的耦合作用,各方程需要同时求解,因此,采用计算机群对模型进行并行求解以缩短收敛时间。当三相的连续性方程残差均小于0.001时,计算可以被终止。
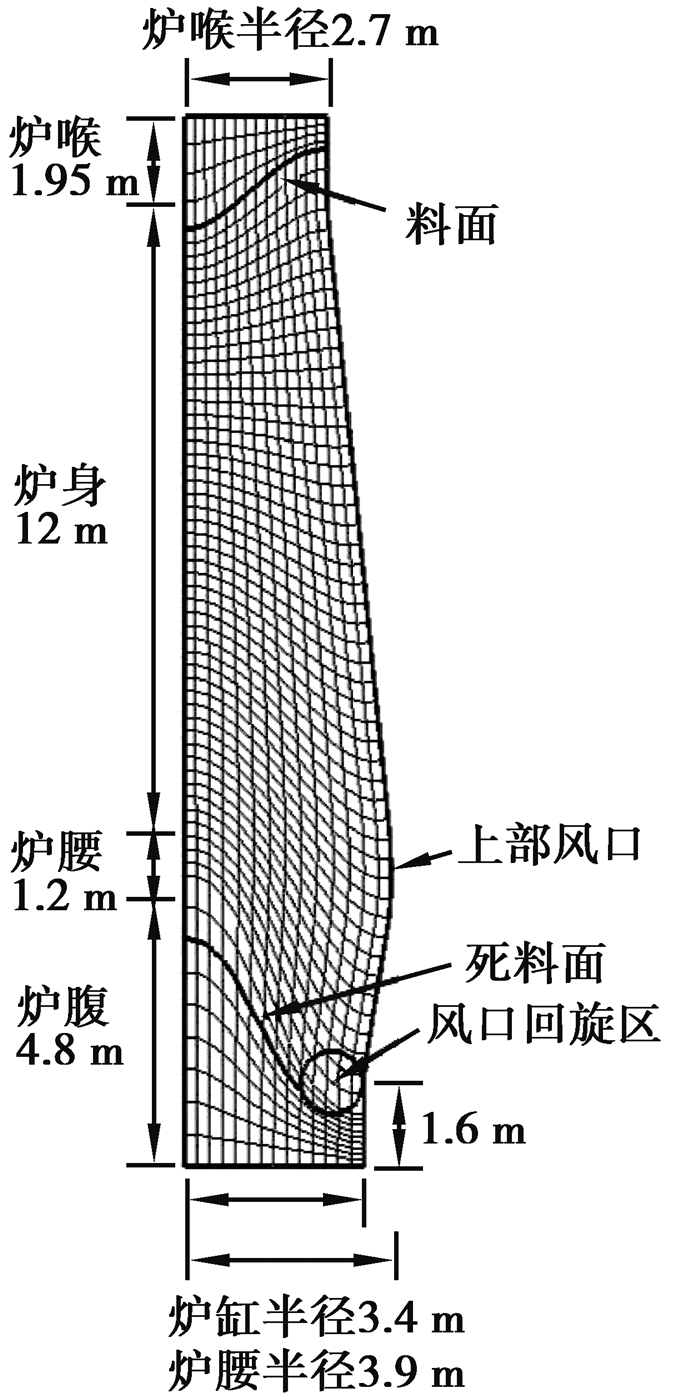
2 数值模拟及模型验证 2.1 高炉结构及计算网格模型以国内某实际生产高炉为研究对象。高炉炉缸直径为6.8 m,高度为19.95 m,有效容积为750 m3,风口为18个。模型假设高炉内型、风口及炉内状况均为轴对称分布,计算二维稳态条件下气液固三相的质量、动量及能量守恒方程。为减少计算量,只计算高炉的半个剖面。在此区域内生成62×14的BFC网格。计算区域划分的网格见图 1。在普通高炉模拟中没有上部风口。
|
图 1 模型中高炉几何参数及计算所用网格 Figure 1 Geometrical parametersand mesh distribution ofblast furnace in the model |
模拟中所设置的普通高炉和氧气高炉的主要操作参数分别如表 3、表 4所示。
| 表 3 普通高炉炉况模拟所用操作参数 Table 3 Operating parameters of traditional blastfurnace in the simulation |
| 表 4 GF-FOBF流程中高炉炉况模拟所用操作参数 Table 4 Operating parameters of the exygen blast furnacein the GF-FOBF process |
在氧气高炉模拟中设置两排风口,炉缸和炉身循环煤气体积、成分和温度如表 5所示。
| 表 5 氧气高炉循环煤气参数 Table 5 Recycling gas parameters of oxygen blast furnace |
本研究对模型计算的结果进行了验证,对比了炉顶气体成分计算值与实际生产中炉顶煤气成分,如表 6所示,可以看到两者之间差距较小,这反映了模型计算结果有较好的可信度。
| 表 6 普通高炉炉顶煤气成分计算值与实测值对比 Table 6 Comparison of calculated top gas compositions andmeasured values of traditional blast furnace |
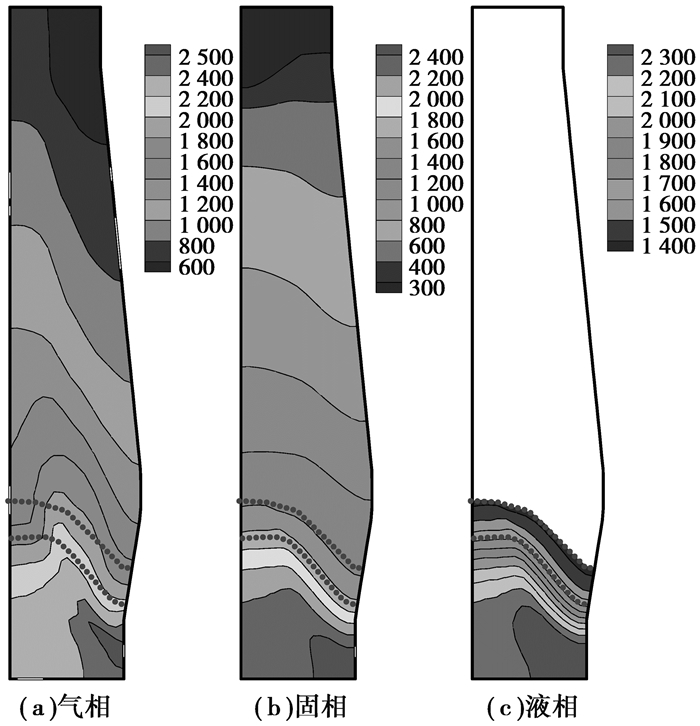
模型计算得到了普通高炉内部温度场、速度场和浓度场等参数的分布情况,图中虚线表示软熔带。图 2为气、固、液三相的温度分布。三相最高温度均在风口回旋区附近。这是由于焦炭及煤粉与鼓风中氧气在此区域发生燃烧反应,释放出大量的热,形成了高炉内部温度场的“焦点”。从图中可以看到软熔带呈倒V型。
|
图 2 普通高炉三相温度场(K) Figure 2 Temperature fields in traditional blast furnace (K) |
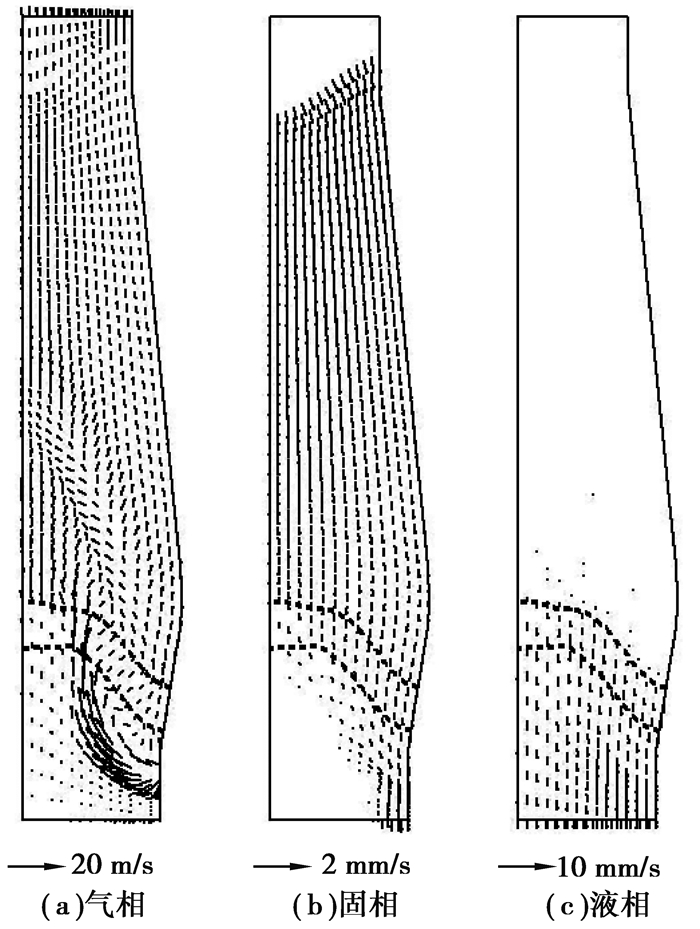
图 3为气、固、液三相速度场。从图中可以清楚地看出软熔带对气相速度的影响情况以及固液相在高炉内的产生和运动情况。气体上升遇到软熔带下沿,由于软熔带中矿石软化,空隙率变小,气流方向在软熔带有一个方向上的突变,反映出软熔带对煤气流的分配作用。固相向下运动是由于矿石熔化以及风口回旋区焦炭的燃烧为其提供了空间。液相的形成始于软熔带,除炉墙处,基本为垂直向下运动,受气流运动影响较小。
|
图 3 普通高炉三相速度场 Figure 3 Velocity fields in traditional blast furnace |
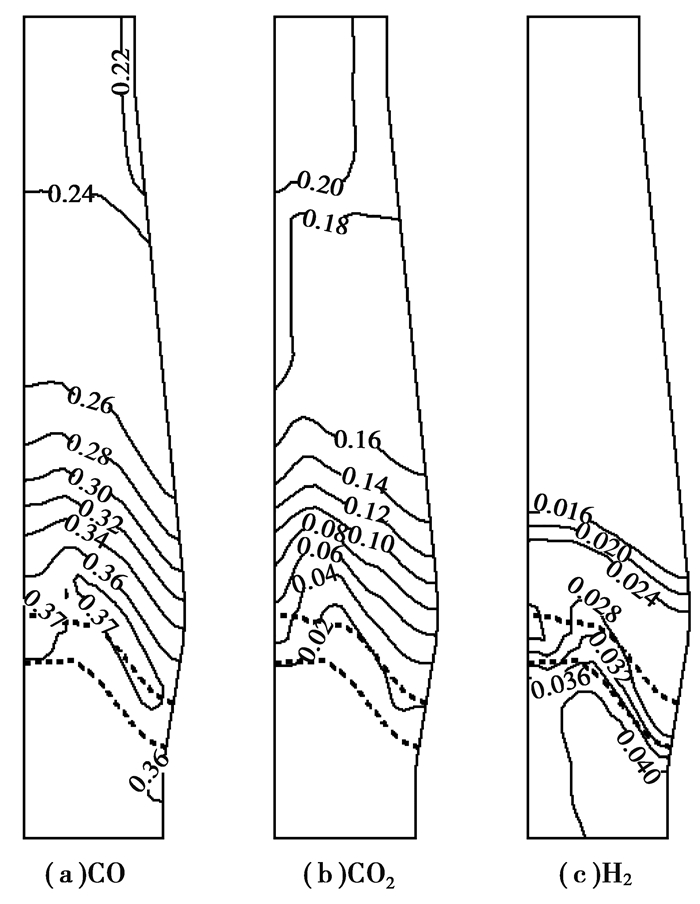
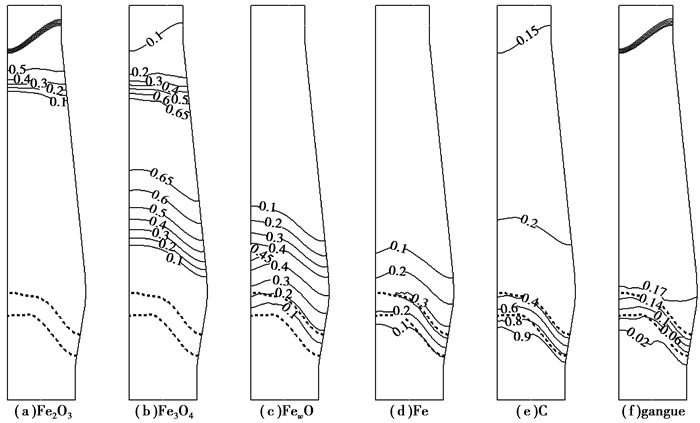
图 4和图 5分别为部分气相组分和固相组分的分布情况,从图中可以清楚地看出矿石在炉内的还原情况以及气体组分在高炉内的变化情况。
|
图 4 普通高炉气相组分体积分数 Figure 4 Volume fraction distributions of gas phase intraditional blast furnace |
|
图 5 普通高炉固相组分质量分数 Figure 5 Mass fraction distributions of solid phase in traditional blast furnace |
应用建立的氧气高炉模型对GF-FOBF流程中的氧气高炉进行了模拟研究。模型计算同样得到了高炉内部温度场、速度场和浓度场等参数的分布情况。从模拟结果中可以发现氧气高炉“上冷下热”的典型特征以及GF-FOBF流程采用双排风口、预热循环煤气解决“上冷下热”问题的效果。
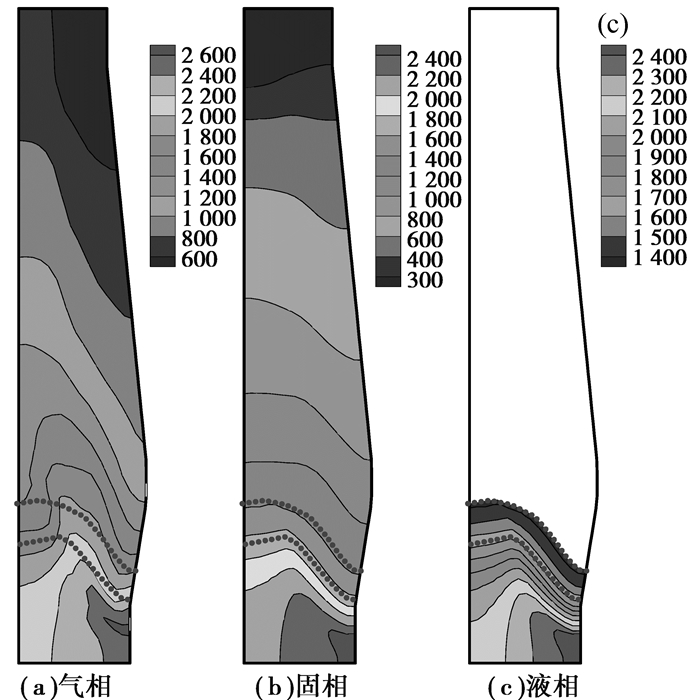
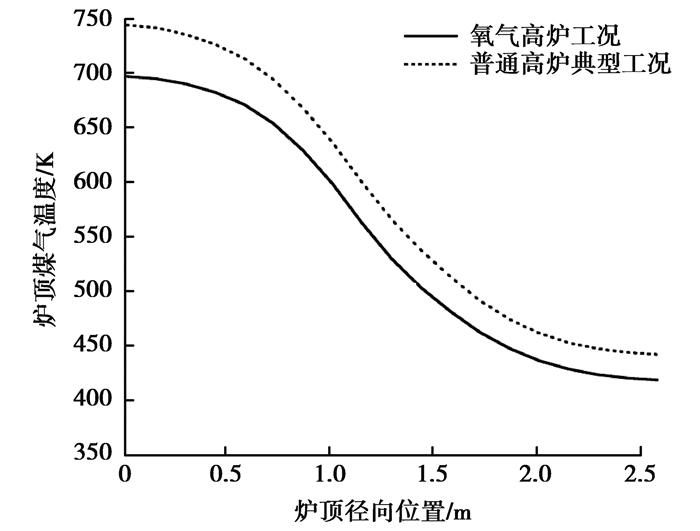
图 6为GF-FOBF流程中氧气高炉三相温度场。由图可见,三相最高温度均在风口回旋区附近,温度变化趋势与普通高炉典型工况相比差别不大。风口最高温度由2 500 K提高到2 600 K左右,炉顶煤气温度略有降低,如图 7所示。
|
图 6 GF-FOBF流程氧气高炉三相温度场(K) Figure 6 Temperature fields in oxygen blastfurnace of GF-FOBF process (K) |
|
图 7 氧气高炉与普通高炉炉顶煤气温度对比 Figure 7 Comparison of top gas temperature betweenoxygen blast furnace and traditional blast furnace |
与典型工况相比,GF-FOBF流程变化幅度较小。这是由于:一方面,炉缸鼓入的循环煤气增加了风口碳素燃烧需加热的煤气总量,降低了风口理论燃烧温度;另一方面,炉身鼓入的循环煤气与炉缸上升煤气汇合,补充了煤气对炉料的加热能力。固相温度场相比典型工况(如图 6(b)所示)并无大的变化。由于炉缸煤气量有所减少,炉缸固相高温区域(Ts≥2 400 K)略有缩小,但软熔带位置及炉身温度场并未发生大的变化,证明GF-FOBF流程较好地解决了氧气高炉“上冷下热”问题。
由于普通高炉炼铁技术已经相当成熟,因此,当采用GF-FOBF流程后,自然希望流程中高炉内部状态不要发生大的改变,这有利于新的工况条件下设备的稳定操作。从三相温度场的角度来看,GF-FOBF流程中高炉风口理论燃烧温度、炉顶煤气温度、软熔带位置及形状等变化不大,这对高炉稳定操作是十分有利的。
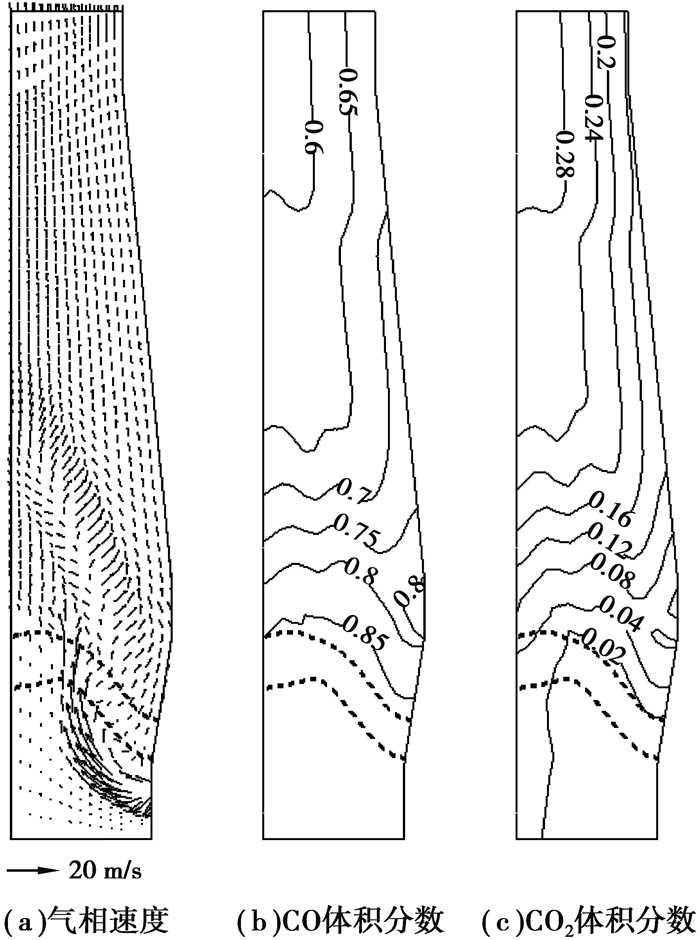
图 8为GF-FOBF流程中高炉气相速度场和气相组分的分布情况。与普通高炉相比,气相速度场发生了一些变化。由图 8可见,炉缸煤气上升穿过软熔带,由于受到软熔带的阻力,煤气方向发生了一些改变,在软熔带上方,炉缸上升煤气完成第三次分配,在径向上进行了重新分布。炉身下部鼓入的循环煤气使得炉墙处煤气在上升过程中偏向炉子中心(普通工况中炉墙处气体则沿着炉墙向上运动)。炉缸煤气与炉身处循环煤气在上升过程中逐渐融合,经过炉身中上部炉料的梳理,平稳地从炉顶排出。固相及液相速度场变化不大,这对于高炉稳定操作也是有利的。
|
图 8 GF-FOBF流程中氧气高炉气相计算结果 Figure 8 Calculated results of gas phase in oxygen blastfurnace of GF-FOBF process |
从图中可以看出各气体组分在高炉内的浓度和分布相比于普通高炉发生了很大的变化,由于上排风口的引入,从上排风口进入的循环煤气的均匀分布成为一个显著的问题,此外,氧气高炉流程中高炉内N2体积分数相比普通高炉明显降低。
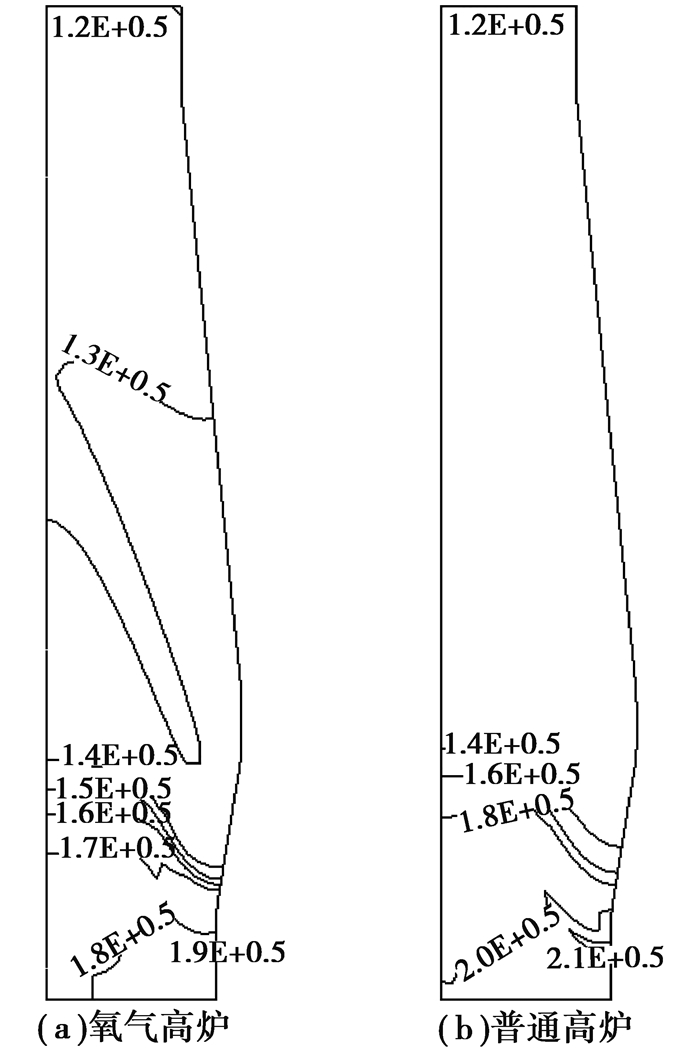
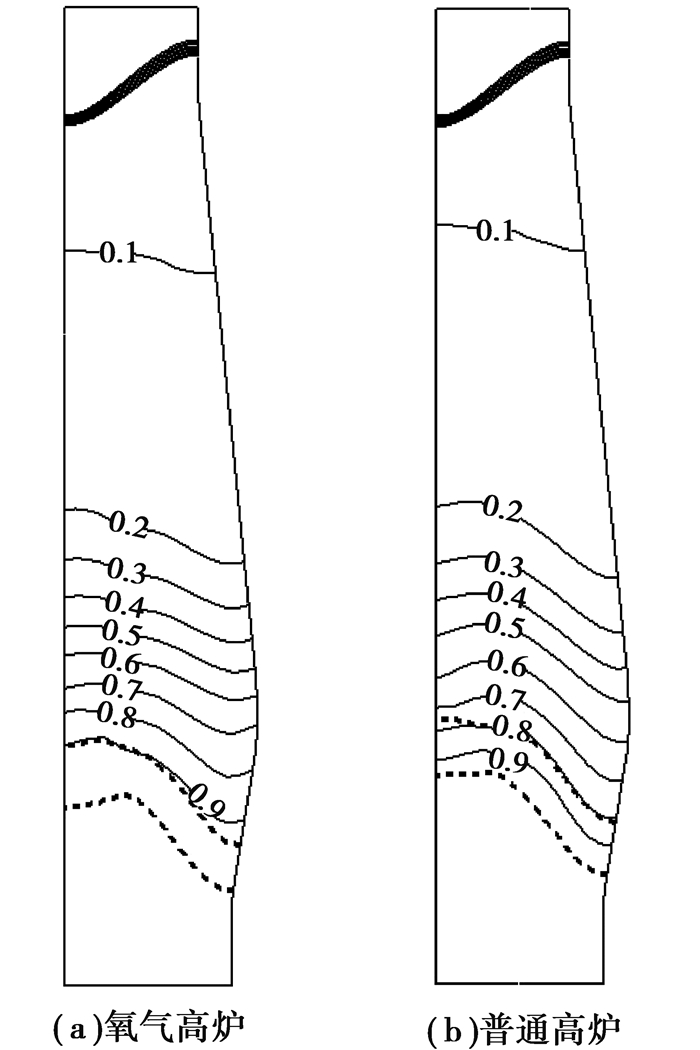
将计算得到的普通高炉和氧气高炉压力场和矿石还原情况进行对比,如图 9、图 10所示,可以发现风口回旋区处气体压力最大,相比普通高炉,由于风口处煤气总量减少,因此,气压有所降低,由2.1×105 Pa降低到1.9×105 Pa。气体在上升过程中压力逐渐降低,但在炉身处并非像普通高炉那样继续呈水平状态逐步降低。由于炉身下部鼓入炉顶循环煤气,因此,上部风口附近气体压力有所提高。炉身循环煤气与炉缸上升煤气在炉子中心汇合,继续上升到炉身上部后气压重新呈水平状态降低,这与气相速度场是相吻合的。与普通高炉典型工况相比,矿石还原度在整个高炉内部均明显提升,在软熔带上沿处已达到0.9左右,说明GF-FOBF流程中高炉内部煤气还原能力增强,间接还原反应得到发展。模型计算得到高炉直接还原度为0.20,相比普通高炉典型工况时的0.50大大降低。
|
图 9 氧气高炉与普通高炉气相压强分布对比(Pa) Figure 9 Comparison of gas pressure between oxygen blastfurnace and traditional blast furnace (Pa) |
|
图 10 氧气高炉与传统高炉矿石还原度分布 Figure 10 Comparison of iron ore reduction degree betweenoxygen blast furnace and traditional blast furnace |
结合热化学模型[17]计算结果,对普通高炉工况及GF-FOBF工况进行对比分析,可以对一些参数的变化规律有更加清晰的认识,具体数据见表 7。
| 表 7 普通高炉与氧气高炉工况参数对比 Table 7 Comparison of operation parameters betweentraditional blast furnace and oxygen blast furnace |
由表 7可见:①随着鼓风氧气浓度提高,焦比逐步降低,煤比逐步提高;②GF-FOBF流程引入气化炉后,需消耗一定量的煤及氧气,但流程整体能耗仍然低于普通高炉;③与普通高炉相比,GF-FOBF流程外供煤气量减少了约50%,但煤气热值提高了约100%,高品质的煤气对提高后续环节利用效率是十分重要的;④GF-FOBF流程需脱除部分CO2及H2O,若能将分离出的CO2进行封存,将大大减少高炉炼铁CO2排放;⑤除以上由热化学模型计算得出的参数外,利用多流体模型可以分析得到GF-FOBF工况高炉利用系数,计算结果显示,GF-FOBF工况利用系数由2.8t/(m3·d)显著提高到4.2 t/(m3·d),将大大提高高炉的生产效率。
4 结语通过对比实际生产数据,证明多流体高炉模型能够很好地反映高炉内部状态。相比于传统高炉,GF-FOBF流程中氧气高炉炉内状态发生一些变化,炉缸温度略有升高,炉身温度有所下降,煤气及压强分布发生变化。但是矿石在高炉内的还原过程加快,间接还原得到发展。通过对比普通高炉和GF-FOBF流程氧气高炉计算得到的各参数分布情况可以发现,GF-FOBF流程基本可以解决“上冷下热”的问题,维持炉内状态的稳定,提高氧气高炉的生产效率,达到良好的节能环保效果。模型可进一步应用于计算和对比各操作参数变化条件下氧气高炉内的状态变化,为氧气高炉参数设计以及流程开发提供有益的参考。
| [1] |
毕学工, 傅连春, 熊玮, 等.
中国炼铁高炉数学模型的研究与应用现状[J]. 过程工程学报, 2010, 10(Suppl): 277–282.
BI Xuegong, FU Lianchun, XIONG Wei, et al. Present status of investigation and application of ironmaking blast furnace mathematical models in china[J]. The Chinese Journal of Process Engineering, 2010, 10(Suppl): 277–282. (in Chinese) |
| [2] | Yagi J. Mathematical modeling of the flow of four fluids in a packed bed[J]. ISIJ international, 1993, 33(6): 619–639. DOI:10.2355/isijinternational.33.619 |
| [3] |
秦民生, 张建良.
高炉氧煤炼铁工艺[J]. 钢铁, 1993, 28(9): 9–13.
QIN Minsheng, ZHANG Jianliang. Oxy-coal technique of blast furnace[J]. Iron and Steel, 1993, 28(9): 9–13. (in Chinese) |
| [4] |
薛庆国, 蓝荣宗, 王静松, 等.
基于氧气高炉的烧结矿还原动力学分析[J]. 重庆大学学报, 2012, 35(11): 67–74.
XUE Qingguo, LAN Rongzong, WANG Jingsong, et al. Kinetics analysis of sinter-reduction base on oxygen blast frnace[J]. Journal of Chongqing University, 2012, 35(11): 67–74. (in Chinese) |
| [5] |
王成善, 时艳文, 李丹丹, 等.
全氧高炉炼铁工艺模拟分析[J]. 重庆大学学报, 2014, 37(9): 47–58.
WANG Chengshan, SHI Yanwen, LI Dandan, et al. Simulation research on oxygen blast furnace ironmaking process[J]. Journal of Chongqing University, 2014, 37(9): 47–58. (in Chinese) |
| [6] | Nogami H, Chu M, Yagi J I. Numerical analysis of blast furnace operations with top gas recycling[J]. Revue de Métallurgie, 2005, 102(3): 189–197. DOI:10.1051/metal:2005132 |
| [7] | Chu M, Yagi J I. Numerical evaluation of blast furnace performance under top gas recycling and lower temperature operation[J]. steel research international, 2010, 81(12): 1043–1050. DOI:10.1002/srin.v81.12 |
| [8] |
储满生, 郭宪臻, 沈峰满, 等.
多流体高炉数学模型的开发和应用[J]. 钢铁, 2007(12): 11–15.
CHU Mansheng, GUO Xianzhen, SHEN Fengman, et al. Development and application of multi-fluid blast furnace model[J]. Iron and Steel, 2007(12): 11–15. (in Chinese) |
| [9] |
储满生, 郭宪臻, 沈峰满, 等.
基于多流体理论的高炉数学模型及其求解[J]. 东北大学学报:自然科学版, 2007, 28(3): 361–364.
CHU Mansheng, GUO Xianzhen, SHEN Fengman, et al. Multi-fluid mathematical model for blast furnace and its solution[J]. Journal of Northeastern University:Natural Science, 2007, 28(3): 361–364. (in Chinese) |
| [10] | Ergun S. Fluid flow through packed columns[J]. Chemical Engineering Progress, 1952, 48(2): 89–94. |
| [11] | Richardson J F, Zaki W N. Sedimentation and fluidization[J]. Transactions of the Institution of Chemical Engineers, 1954, 32(1): 35–53. |
| [12] | Carman P C. Fluid flow through a granular bed[J]. Transactions of the Institution of Chemical Engineers, 1937, 15(3): 150–166. |
| [13] | Ranzand W E, Marshall W R. Evaporation from drops[J]. Chemical Engineering Progress, 1952, 48(3): 141–180. |
| [14] | Mackey P J, Warner N A. Heat transfer between dispersed liquid metals and gases in packed beds[J]. Metallurgy Transactions, 1972, 3(7): 1792–1807. |
| [15] | Eckert E R G, Drake R M. Heat and mass transfer (2nd Edition)[M]. NewYork, McGrawHill: 1959: 173. |
| [16] | Cham L. Phoenics user docunment[M]. London: CHAM Ltd., 2000. |
| [17] | Meng J L, Tang H Q, Guo Z C. Comprehensive Mathematical Model of Full Oxygen Blast Furnace with Top Recycle Gas Heated by Gasifier[J]. Applied Mechanics & Materials, 2013, 268-270: 356–364. |
 2015, Vol. 38
2015, Vol. 38


