近年来,随着石油资源的短缺及人们环保意识的增强,世界各国都在环境保护和节约资源上做出巨大努力,尤其在汽车行业,人们越来越重视绿色环保汽车的开发和利用,在这种形势下,混合动力汽车由于其油耗小、工作效率高、续航能力强的优点,引起了人们的广泛关注[1-3]。双向DC/DC变换器作为混合动力汽车能量流动中的核心一环,搭建起了混合动力汽车中动力电池和直流母线双向能量流通桥梁,是研究和开发混合动力汽车发展的重点领域之一。因此,混合动力汽车中双向DC/DC变换器拓扑结构及其控制策略倍受专家和学者的关注[4-10]。
目前,已有很多智能算法被应用到双向DC/DC变换器的控制系统当中,诸如滑膜控制、单周期控制、神经网络控制、自适应控制等,上述这些控制算法各具优点,但都不能兼具动态响应快、鲁棒性强、稳定性好的特点,在实际应用中存在缺陷。基于此,笔者提出将智能控制领域中的模糊控制与PI控制相结合,用于混合动力汽车的双向DC/DC变换器的控制当中,以提高控制系统的性能。同时,考虑到混合动力汽车要求双向DC/DC变换器重量轻、体积小、工作效率高、稳定性和动态响应能力强,选用双向Buck/Boost变换器作为主电路拓扑结构,最后进行仿真和实验验证。
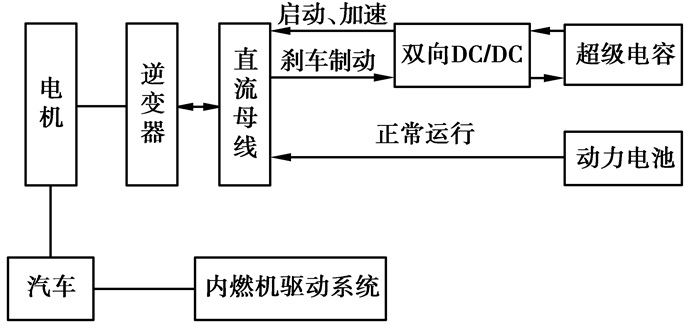
1 工作原理与主电路拓扑结构图 1为典型的混合动力汽车的电路系统,当汽车突然启动、加速时,双向DC/DC变换器工作于Boost模式,由超级电容提供瞬时的大功率;当汽车刹车制动时,双向DC/DC变换器工作于Buck模式,将制动产生的多余能量迅速存储起来[11-13]。
|
图 1 混合动力汽车的电路系统 Figure 1 Circuit system of Hybrid electric vehicle |
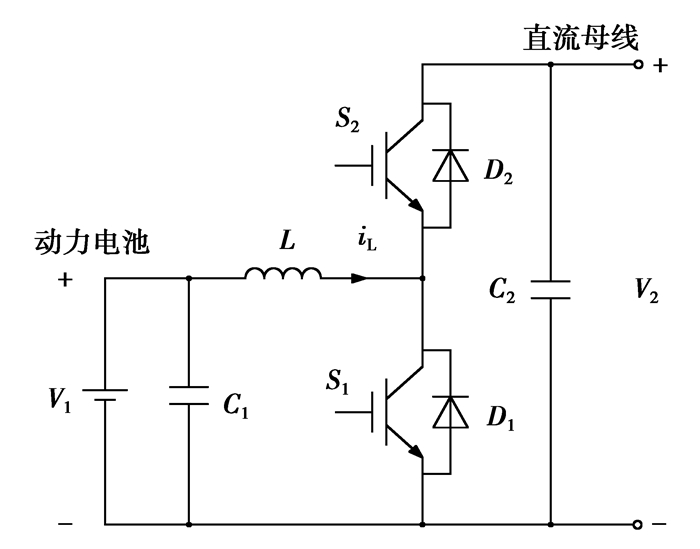
选用双向Buck/Boost变换器电路的拓扑结构,如图 2所示,正常工作时两个功率互补导通。当变换器处于Boost模式时,能量由V1流向V2,此时功率开关管S1导通,S2截止;当变换器处于Buck模式时,能量由V2流向V1,此时功率开关管S2导通,S1截止,D1、D2在变换器工作中充当续流二极管。与其他类型双向直流变换器相比,双向Buck/Boost变换器的电压应力、电流应力最小,工作过程中开关损耗小,在大功率场合仍能保持较高的工作效率。
|
图 2 双向Buck/Boost变换器的电路拓扑图 Figure 2 Circuit topology of bi-directional Buck/Boost converter |
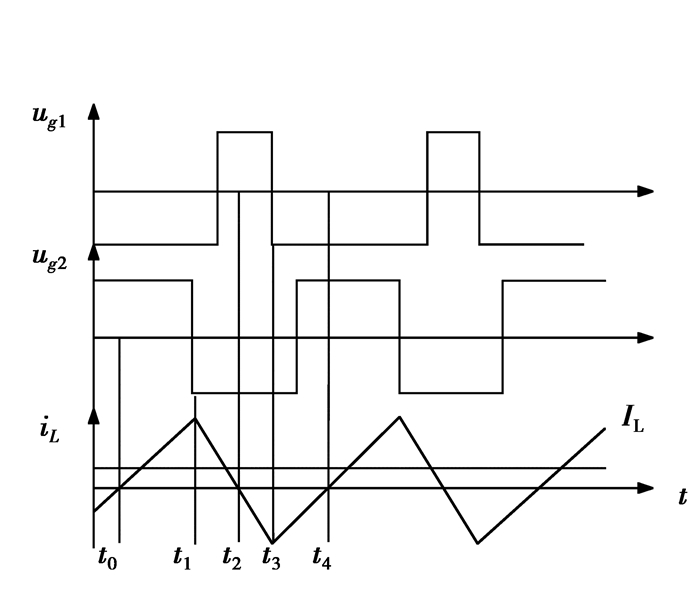
双向Buck/Boost变换器工作波形如3图所示,由图可知,在变换器工作过程中,储能电感L电流方向有正有负,电感电流在一个工作周期内可以分为4种工作状态,其中ug1、ug2为变换器两开关信号,iL为电感电流[14]。
|
图 3 双向Buck/Boost变换器的工作波形 Figure 3 The working waveform of the bidirectional Buck/Boost converter |
工作状态1(t0~t1):电感电流IL在t0时刻由负变正,二极管D1自然关断,双向Buck/Boost变换器工作在Boost模式。
工作状态2(t1~t2):电感电流IL在t1时刻达到峰值,IGBTS2实现零电压开通,IGBTS1关断,二极管D2续流,期间动力电池和储能电感同时向直流母线端提供能量。
工作状态3(t2~t3):电感电流IL在t2时刻由正变负,双向Buck/Boost变换器工作在Buck模式,二极管D2自然关断,电感电流IL反向增大直到IGBTS2关断。
工作状态4(t3~t4):t3时刻二极管D1续流,电感电流IL正向增大,在这个过程中IGBTS1实现零电压开通,到t4时刻电感电流IL为0,二极管D1自然关断,一个周期结束。
这种开关控制方式不仅通过半导体开关器件实现软开关控制功能,还可以有效避免二极管反向恢复时引起的电流尖峰。
根据笔者设计要求,变换器的电路参数设置为:电感L=1.3 mH、电容C1=C2=3 300μF/800 V、功率开关管选择FF75R12RT4型IGBT、开关频率设定为10 kHz。
2 系统建模 2.1 Boost模式下的模型建立当变换器工作于Boost模式时,由超级电容提供混合动力汽车所需的瞬时大功率,负载为动力电池。为了计算方便,这里可以近似认为输入电压为V1,输出电压为V2,等效负载阻值为R。可求得Boost模式下双向Buck/Boost变换器的小信号数学模型为
| $ \left\{ \begin{array}{l} L\frac{{{\rm{d}}{{\hat i}_{\rm{L}}}\left( T \right)}}{{{\rm{d}}t}} = {{\hat v}_1}\left( t \right) + {V_2}\hat d\left( t \right) - \left( {1 - D} \right){{\hat v}_2}\left( t \right),\\ {C_2}\frac{{{\rm{d}}{{\hat v}_2}\left( t \right)}}{{{\rm{d}}t}} = \left( {1 - D} \right){{\hat i}_{\rm{L}}}\left( t \right) - {I_{\rm{L}}}\hat d\left( t \right) - \frac{{{{\hat v}_2}\left( t \right)}}{R}; \end{array} \right. $ | (1) |
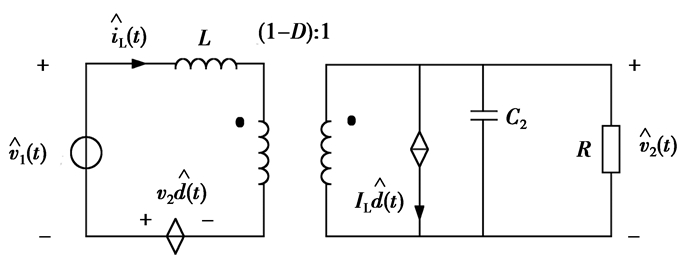
由式(1)可建立变换器在Boost模式下的小信号模型,如图 4所示。
|
图 4 Boost模式下变换器的小信号交流等效电路 Figure 4 Small signal ac equivalent circuit under Boost mode |
求得Boost模式下
| $ {G_{i{\rm{d}}}}\left( s \right) = \frac{{{{\hat i}_{\rm{L}}}\left( s \right)}}{{\hat d\left( s \right)}}\left| {_{{{\hat v}_1}\left( s \right) = 0}} \right. = \frac{{{V_2}{C_2}s + \frac{{2{V_2}}}{R}}}{{L{C_2}{s^2} + \frac{L}{R}s + 2{{D'}^2}}}。$ | (2) |
| $ {G_{vi}}\left( s \right) = \frac{{{{\hat v}_{\rm{2}}}\left( s \right)}}{{{{\hat i}_{\rm{L}}}\left( s \right)}}\left| {_{{{\hat v}_1}\left( s \right) = 0}} \right. = \frac{{\left( {1 - D} \right) - \frac{{sL}}{{\left( {1 - D} \right)R}}}}{{{C_2}s + \frac{2}{R}}}。$ | (3) |
当变换器工作于Buck模式时,由动力电池供电,此时负载为超级电容。为了计算方便,这里可以近似认为输入端电压为V2,输出电压为V1,等效负载阻值为R。可求得Buck模式下变换器的小信号数学模型为
| $ \left\{ \begin{array}{l} L\frac{{{\rm{d}}{{\hat i}_{\rm{L}}}\left( T \right)}}{{{\rm{d}}t}} = D{{\hat v}_2}\left( t \right) + {V_2}d\left( t \right) - {{\hat v}_1}\left( t \right),\\ {C_1}\frac{{{\rm{d}}{{\hat v}_1}\left( t \right)}}{{{\rm{d}}t}} = {{\hat i}_{\rm{L}}}\left( t \right) - \frac{{{{\hat v}_1}\left( t \right)}}{r}。\end{array} \right. $ | (4) |
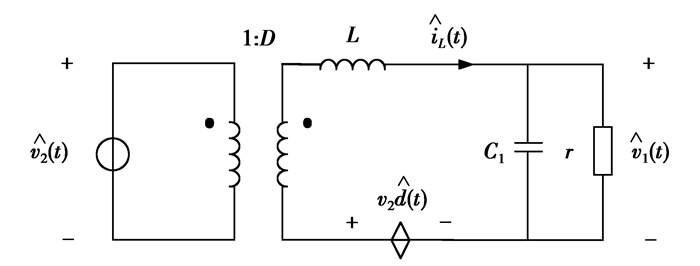
由式(4)可建立变换器在Buck模式下的小信号模型,如图 5所示。
|
图 5 Buck模式下变换器的小信号交流等效电路 Figure 5 Small signal ac equivalent circuit under Buck mode |
求得Buck模式下
| $ {G_{i{\rm{d}}}}\left( s \right) = \frac{{{{\hat i}_{\rm{L}}}\left( s \right)}}{{\hat d\left( s \right)}}\left| {_{{{\hat v}_2}\left( s \right) = 0}} \right. = \frac{{{V_2}{C_1}s + \frac{{{V_2}}}{r}}}{{L{C_1}{s^2} + \frac{L}{r}s + 1}}。$ | (5) |
电感电流
| $ {G_{vi}}\left( s \right) = \frac{{{{\hat v}_{\rm{1}}}\left( s \right)}}{{{{\hat i}_{\rm{L}}}\left( s \right)}}\left| {_{{{\hat v}_2}\left( s \right) = 0}} \right. = \frac{1}{{{C_1}s + \frac{1}{r}}}。$ | (6) |
混合动力汽车在行驶过程中,会频繁地进行加速、减速、启动和制动,在此过程中电机的母线电压和电流不停地发生变化,双向Buck/Boost变换器能量流动的方向也在不断变化[15-16]。
当双向Buck/Boost变换器处于Boost工作模式时,超级电容提供瞬时大功率,需引入直流母线电压外环来保持母线电压稳定,从而改善牵引电机的运行特性,同时为了提高变换器的动态响度引入电感电流内环;当双向Buck/Boost变换器处于Buck工作模式时,超级电容回收制动产生的多余能量,为了防止母线电压过高以至于损坏变换器,考虑引入直流母线电压外环,同时引入电感电流内环以提高变换器的动态响应能力。
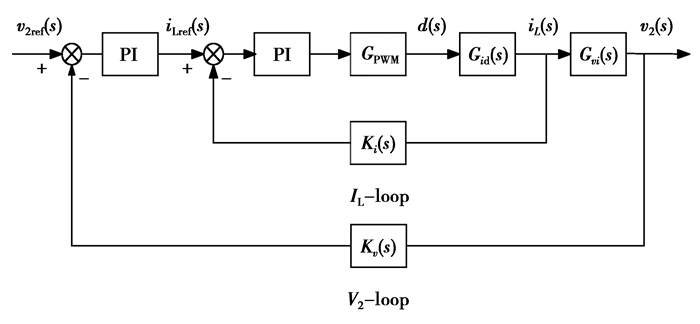
因此,笔者的双向Buck/Boost变换器采用直流母线电压作为外环、电感电流作为内环的双闭环控制结构。考虑到模拟控制器离散化带来的延时会导致系统不稳定,这里采用PI控制器来改善系统能量,系统的控制框图如图 6所示。
|
图 6 系统的控制结构框图 Figure 6 Control structure diagram of the system |
由于Buck模式和Boost模式下PI控制器设计过程类似,笔者就Boost模式下电压外环、电流内环PI控制器参数的计算作详细介绍。设定电流内环的穿越频率fci=1 kHz,转折频率fni=200 Hz。
由图 6可知,未经PI控制器补偿的电流内环原始回路增益函数为
| $ {G_i}\left( s \right) = {G_{{\rm{PWM}}}}{G_{id}}\left( s \right){K_i}\left( s \right)。$ | (7) |
设PI控制器传递函数为
| $ {G_{{\rm{PI}}i}} = \frac{{{K_{{\rm{P}}i}}s + {K_{Ii}}}}{s}。$ | (8) |
列出下面方程组:
| $ \left\{ \begin{array}{l} \frac{{{K_{{\rm{I}}i}}}}{{2{\rm{ \mathsf{ π} }}{K_{{\rm{P}}i}}}} = {f_{ni}},\\ {\left| {{G_i}\left( s \right){G_{{\rm{PI}}i}}\left( s \right)} \right|_{s = j2{\rm{ \mathsf{ π} }}f{\rm{c}}i}} = 1; \end{array} \right. $ | (9) |
代入相关数据可得:KPi=0.048,KIi=60.5。
对电压外环进行PI控制器设计时,可以将电流内环看做一个比例环节,比例系数Kvi=1/Ki(s)。设定电压外环的穿越频率fcv=100 Hz,转折频率为fnv=10 Hz。
对于未经PI控制器补偿的电压外环原始回路增益函数为
| $ {G_v}\left( s \right) = {G_{vi}}\left( s \right){K_v}\left( s \right)\frac{1}{{{K_i}\left( s \right)}}, $ | (10) |
电压外环PI控制器的传递函数为
| $ {G_{{\rm{PI}}v}} = \frac{{{K_{Pv}}s + {K_{Iv}}}}{s}, $ | (11) |
列出下面方程组:
| $ \left\{ \begin{array}{l} \frac{{{K_{{\rm{I}}v}}}}{{2{\rm{ \mathsf{ π} }}{K_{{\rm{P}}v}}}} = {f_{nv}},\\ {\left| {{G_v}\left( s \right){G_{{\rm{PI}}v}}\left( s \right)} \right|_{s = j2{\rm{ \mathsf{ π} }}f{\rm{c}}v}} = 1。\end{array} \right. $ | (12) |
代入相关数据可得:KPv=0.37,KIv=23.25。
3.2 改进PI控制器混合动力汽车双向DC/DC变换器具有较快的响应速度和较强的鲁棒性,3.1节设计的PI控制器能够满足稳态无静差的要求,但系统的稳定性和动态响应能力有待进一步改善。模糊控制器可以很好地消除系统内部参数变化及外部干扰对控制效果的影响,而且响应速度快、动态性能好。将模糊控制和PI控制两种控制算法结合起来应用于混合动力汽车双向DC/DC变换器中,可以有效提高变换器的响应速度、稳定性和鲁棒性。
笔者设计的模糊PI控制器由输入和输出变量、模糊控制器和PI控制器组成,系统的结构图如图 7所示。

|
图 7 模糊PI闭环控制框图 Figure 7 Fuzzy PI closed loop control block diagram |
笔者设计的模糊控制器有两个输入变量,分别是采样电压与参考电压的偏差e和偏差变化率Δe,输出变量是PI控制器的两个参数:ΔKP、ΔKI。首先采用Mamdani提出的标准化设计方法对控制系统的论域进行模糊化,设定e和Δe的变化范围为{-3,-2,-1, 0, 1, 2, 3},PI控制器3个参数的变化范围:ΔKP={-0.3,-0.2,-0.1, 0, 0.1, 0.2, 0.3}, ΔKI={-0.06, -0.04, -0.02, 0, 0.02, 0.04, 0.06}, 系统模糊子集为[NB,NM,NS,ZO,PS,PM,PB],分别与[负大,负中,负小,零,正小,正中,正大]相对应。
模糊规则库的建立是模糊控制的重点,笔者根据电压偏差e和偏差变化率Δe的变化情况,从而确定PI参数的调整规律,模糊规则为“if then”条件语句。
PI控制器参数的模糊控制规则如表 1所示,控制器在运行时不断查询设置好的控制规则,计算出相应的控制输出量ΔKP、ΔKI。
| 表 1 PI控制器的ΔKP/ΔKI模糊控制规则 Table 1 Fuzzy control rules for controllers |
根据双向DC/DC变换器在工程应用中的实际情况,这里采用三角形隶属函数形式进行分析,并采用重心法对控制输出量解模糊后得到模糊PI控制器的控制参数为
| $ \left\{ \begin{array}{l} {K_{\rm{P}}} = K_{\rm{P}}^0 + \Delta {K_{\rm{P}}},\\ {K_{\rm{I}}} = K_{\rm{I}}^0 + \Delta {K_{\rm{I}}}; \end{array} \right. $ |
式中:KP0、KI0为PI控制器的初始设置值。
4 仿真分析在MATLAB/SIMULINK7.1环境中构建双向Buck/Boost变换器模型,由于Buck模式和Boost模式结果基本一致,对Boost模式进行仿真结果分析。电路参数设置为:L=1.3 mH,C1=C2=3 300 μF,U1=260 V,U2=560 V,fs=10 kHz。
双向DC/DC变换器在Boost模式下采用PI控制器补偿前后系统的输出电压波形如图 8所示,由图可以看出,变换器控制系统的电压外环、电流内环采用PI控制器补偿后,其输出电压的超调量、稳态误差得到了很大的改善,系统的稳定性和动态响应能力提高。

|
图 8 Boost模式下的输出电压波形 Figure 8 Voltage output waveform under Boost mode |
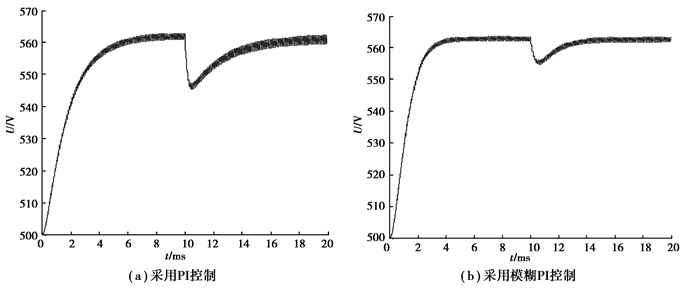
当变换器满载启动时,在t=10 ms时突然增大负载,用来模拟混合动力汽车突然启动、加速的情况,仿真结果如图 9所示。
|
图 9 Boost模式下负载增加时输出电压波形 Figure 9 Voltage output waveform when load increases under Boost mode |
由图 9可知,电压外环使用PI控制时,输出电压的幅值变化为16 V,需要10 ms左右才能再次达到平衡;当电压外环使用模糊PI控制时,输出电压的幅值变化为8 V,恢复到原来的值只需要4 ms。仿真结果表明模糊PI控制具有更强的稳定性和鲁棒性,系统的控制精度和动态响应速度都有很大的提高。
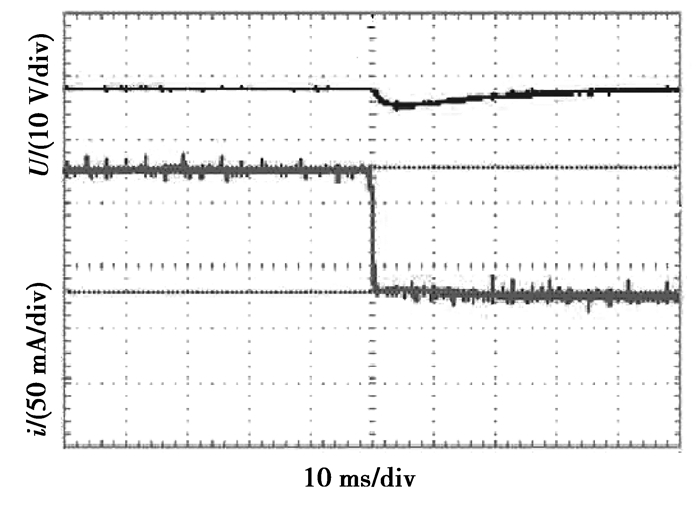
5 实验验证以M9713为控制核心建立一个小功率实验平台,对设计的实验样机进行Boost模式时的动态实验。与仿真过程类似,这里通过改变负载的大小来模拟混合动力汽车突然启动或加速时的情况,在2 s时增加负载的值,得到输出电压和输出电流波形如图 10所示。
|
图 10 Boost模式下负载增加时实验波形 Figure 10 Experiment waveform when load increases under Boost mode |
由图 10可知,变换器在20 ms内再次达到平衡状态,而且负载突然增加时输出电压的幅值变化较小,表明基于模糊PI控制的双向DC/DC变换器具有动态响应快、鲁棒性强的优点。
实验过程中测出的变换器在Boost工作模式下的电压、电流、功率的数据如表 2所示。
| 表 2 实验数据 Table 2 Experiment data |
从表中数据可知,变换器电压外环采用模糊PI控制器时,系统具有较高的工作效率,可以有效减小损耗、节约资源,具有较强的实用价值。
6 结论根据混合动力汽车对变换器的要求,选取双向Buck/Boost变换器作为主电路拓扑,通过半导体器件实现了软开关技术,并引入模糊控制算法,对PI控制器进行了改进。模糊控制增强了系统的动态性能和鲁棒性,PI控制稳定性好、调整方便,两种控制方式结合在一起使系统的控制效果更好。
仿真和实验结果表明,笔者设计的双向DC/DC变换器,具有良好的稳态性和鲁棒性,在混合动力汽车中具有较强的实用价值。如何使变换器与混合动力汽车的能量管理系统相兼容,将是下一步研究的方向。
| [1] |
舒红, 蒋勇, 高银平.
中度混合动力汽车模型预测控制策略[J]. 重庆大学学报, 2010, 33(1): 36–41.
SHU Hong, JIANG Yong, GAO Yinpin. Model predictive control strategy of a medium hybrid electric vehicle[J]. Journal of Chongqing University, 2010, 33(1): 36–41. (in Chinese) |
| [2] |
陆治国, 祝万平, 刘捷丰, 等.
一种新型交错并联双向DC/DC变换器[J]. 中国电机工程学报, 2013, 33(12): 39–46.
LU Zhiguo, ZHU Wanping, LIU Jiefeng, et al. A novel interleaved parallel bidirectional DC/DC converter[J]. Proceedings of the CSEE, 2013, 33(12): 39–46. (in Chinese) |
| [3] |
杨亚联, 陈方元, 秦大同, 等.
混合动力汽车用DC-DC和IPU散热结构优化[J]. 重庆大学学报, 2010, 33(7): 1–6.
YANG Yalian, CHEN Fangyuan, QIN Datong, et al. Heat dissipation optimization of DC-DC and IPU for hybrid electric vehicle[J]. Journal of Chongqing University, 2010, 33(7): 1–6. DOI:10.11835/j.issn.1000-582X.2010.07.001 (in Chinese) |
| [4] | Erb D C, Onar O C, Khaligh A. Bi-directional charging topologies for plug-in hybrid electric vehicles[C]//Applied Power Electronics Conference and Exposition, Feb 21-25, 2010, Palm Springs, CA, USA. [S. l. ]: IEEE, 2010: 2066-2072. |
| [5] |
赵成勇, 李路遥, 翟晓萌, 等.
新型模块化高压大功率DC/DC变换器[J]. 电力系统自动化, 2014, 38(4): 72–78.
ZHAO Chengyong, LI Luyao, ZHAI Xiaomeng, et al. A new type of modular high-voltage high-power DC-DC converter[J]. Automation of Electric Power Systems, 2014, 38(4): 72–78. DOI:10.7500/AEPS20130530014 (in Chinese) |
| [6] | Zhang J, Kim R Y, Lai J S. High-power density design of a soft-switching high-power bidirectional DC-DC converter[C]//Power Electronics Specialists Conference, 2006. Pesc'06. IEEE. IEEE, 2017. |
| [7] |
周美兰, 田小晨.
用于电动汽车的交错并联软开关双向DC/DC变换器[J]. 哈尔滨理工大学学报, 2016, 21(4): 83–89.
ZHOU Meilan, TIAN Xiaochen. An Interleaved Soft-switching Bidirectional DC/DC Converter in Electric Vehicles[J]. Journal of Harbin University of Science & Technology, 2016, 21(4): 83–89. (in Chinese) |
| [8] | Han S, Divan D. Bi-directional DC/DC converters for plug-in hybrid electric vehicle (PHEV) applications[C]//IEEE. IEEE, 2008: 784-789. |
| [9] | Inoue S, Akagi H. A bidirectional DC-DC converter for an energy storage system with galvanic isolation[J]. IEEE Transactions on Power Electronics, 2007, 22(6): 2299–2306. DOI:10.1109/TPEL.2007.909248 |
| [10] | Zhang J, Lai J S, Yu W. Bidirectional DC-DC converter modeling and unified controller with digital implementation[C]//IEEE. IEEE, 2008: 1747-1753. |
| [11] |
孙鹤旭, 张厚升.
两并联双向DC/DC变换器的滑模变结构控制[J]. 电力电子技术, 2016, 50(5): 4–8.
SUN Hexu, ZHANG Housheng. Sliding mode control strategy for interleaved bi-directional DC/DC converter[J]. Power Electronics, 2016, 50(5): 4–8. (in Chinese) |
| [12] | Yu W, Qian H, Lai J S. Design of high-efficiency bidirectional DC-DC converter and high-precision efficiency measurement[C]//Industrial Electronics, 2008. IECON 2008. Conference of IEEE. IEEE, 2009. |
| [13] | He L, Zou D, Wu T. Buck converter based on One-cycle control and PD control[C]//The 7th World Congress on Intelligent Control and Automation. 2008: 3235-3238. |
| [14] | Shi X, Xu Z. Research on One-cycle control for buck converter[C]//International Conference on Electric Information and Control Engineering. IEEE, 2011: 1649-1651. |
| [15] | Guo Y, Zhang C, Wang Z, et al. Study on the method of fuzzy PID control for DC/DC converter[C]//International Conference on Information NETWORKING and Automation. IEEE, 2010: V1-329-V1-332. |
| [16] |
孙文, 林平, 卢冶, 等.
用于电动汽车的双向DC/DC变换器控制设计[J]. 电力电子技术, 2012, 46(7): 40–42.
SUN Wen, LIN Ping, LU Ye, et al. Control design of a bi-directional DC/DC converter for electric vehicle[J]. Power Electronics, 2012, 46(7): 40–42. (in Chinese) |
 2018, Vol. 41
2018, Vol. 41


 ,
,